Descripción

Posición relativa de dos planos.

Ángulo entre dos planos.

Un ángulo entre dos planos se define como el ángulo entre los vectores normales de los planos.

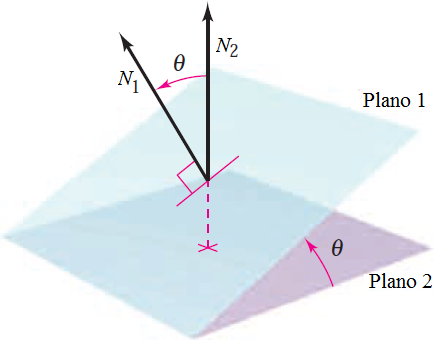
Si los vectores normales de los planos 1 y 2 son N₁ y N₂ respectivamente, entonces el ángulo entre los planos es:

\( \displaystyle \cos\theta = \frac{\mathbf{N}_1\cdot \mathbf{N}_2}{\|\mathbf{N}_1\| \cdot\|\mathbf{N}_2\|}\)

El ángulo entre dos planos está referido al menor ángulo entre dichos planos. La medida del menor ángulo está dada por:

\( \displaystyle \cos\theta = \frac{|\mathbf{N}_1\cdot \mathbf{N}_2|}{\|\mathbf{N}_1\| \cdot\|\mathbf{N}_2\|}\)

 

Planos paralelos en R³.

Dos planos son paralelos en R³ si y sólo si sus vectores normales son paralelos.

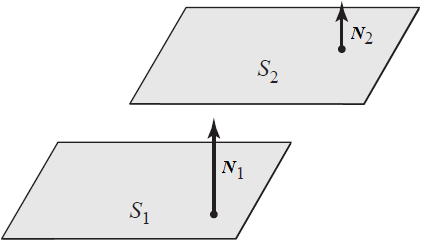
Criterio: N₁ = α N₂ ó N₁ × N₂ = 0.

Planos perpendiculares en R³.

Dos planos son perpendiculares en R³ si y sólo si sus vectores normales son ortogonales.

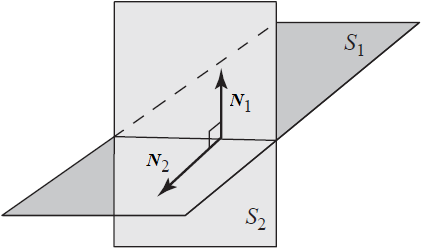
Criterio: N₁ . N₂ = 0.

Ecuación general de planos perpendiculares a los planos coordenados ó paralelos a los ejes coordenados.

Plano perpendicular al plano x y (o paralelo al eje z): a x + b y + d = 0.

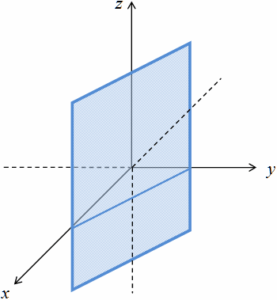
Plano perpendicular al plano x z (o paralelo al eje y): a x + c z + d = 0.

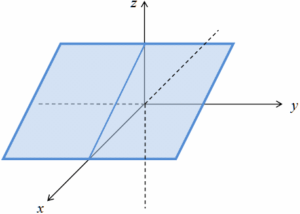
Plano perpendicular al plano y z (o paralelo al eje x): b y + c z + d = 0.

Una ecuación lineal que contiene únicamente dos variables representa un plano perpendicular al plano coordenado de esas dos variables, y es paralelo al eje coordenado a lo largo del cual se mide la variable que no aparece en la ecuación, y recíprocamente.

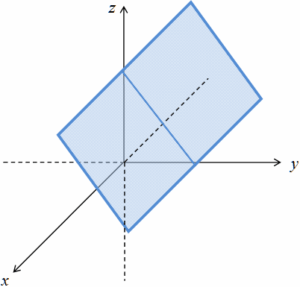
Planos que contienen a los ejes de coordenadas.

En las tres ecuaciones anteriores, si d = 0 se obtienen planos que contienen a los ejes z, y y x respectivamente.

Plano que contiene al eje x: b y + c z = 0.

Plano que contiene al eje y: a x + c z = 0.

Plano que contiene al eje z: a x + b y = 0.

Ecuación general de los planos paralelos a los planos coordenados ó perpendiculares a los ejes coordenados:

Cuando un plano es paralelo a un plano coordenado, las componentes del vector normal sobre los ejes que contienen al plano coordenado son cero y sobre el eje no contenido en el plano coordenado es la unidad.

< 0 , 0 , 1 > es el vector normal de un plano paralelo al plano x y (perpendicular al eje z):

c z + d = 0.

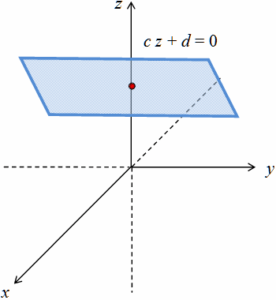
< 0 , 1 , 0 > es el vector normal de un plano paralelo al plano x z (perpendicular al eje y):

b y + d = 0.

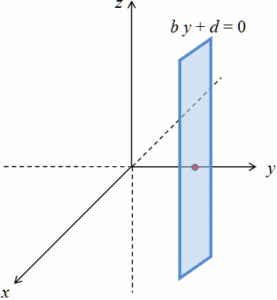
< 1 , 0 , 0 > es el vector normal de un plano paralelo al plano y z (perpendicular al eje x):

a x + d = 0.

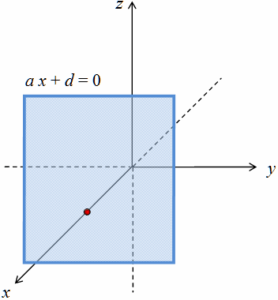
Una ecuación lineal en una sola variable representa un plano perpendicular al eje coordenado a lo largo del cual se mide con esa variable y paralelo al plano de las dos variables que no figuran en la ecuación, y recíprocamente.