Descripción
Función parte entera de x.
Definición de la función parte entera.
La función parte entera de x, denotada por ⟦ x ⟧ está definida como:
y = f (x) = ⟦ x ⟧ = n si n ≤ x < n + 1
El resultado que se obtiene al calcular la parte entera de un número es el entero menor o igual al número dado. En base a lo anterior:
| ⟦ 2 ⟧ = 2 | ⟦ 4.3 ⟧ = 4 |
| ⟦ 1.999 ⟧ = 1 | ⟦ – 3 ⟧ = – 3 |
| ⟦ – 1.5 ⟧ = – 2 | ⟦ – 4.001 ⟧ = – 5 |
| \( [\vert \, \frac{3}{4} \, \vert] = 1\) | \( [\vert -\frac{7}{3} \, \vert] = -3\) |
| ⟦ π ⟧ = 3 | \( [\vert \, \sqrt{3} \, \vert] = 1\) |
| \( [\vert \, 1+\sqrt{5} \, \vert] = 3\) | \( [\vert \, 3-\sqrt{12} \, \vert] = -1\) |
| \( [\vert -2-\sqrt{7} \, \vert] = -5\) | \( \left[\big\vert \, \frac{6-5\,\sqrt{3}}{2} \, \big\vert\right] = -2\) |
Dominio de la función parte entera.
Dom f = ℝ
Gráfico de la función parte entera.
Asignándole valores enteros a “n”, se determina el intervalo de aplicación de x. A continuación se muestran algunos valores de n con su respectiva gráfica.
f (x) = ⟦ x ⟧ = n si n ≤ x < n + 1
Sea n = – 4. De acuerdo con la definición anterior:
f (x) = – 4 si – 4 ≤ x < – 4 + 1
si – 4 ≤ x < – 3
Esto se interpreta diciendo que si – 4 ≤ x < – 3, entonces f (x) es una función constante, f (x) = – 4. La gráfica una recta horizontal.
La gráfica de la función f (x) = ⟦ x ⟧ en el intervalo – 4 ≤ x < – 3 es:
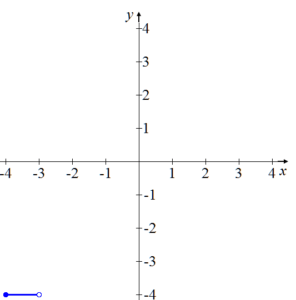
Obsérvese que el punto ( – 4 , – 4 ) pertenece a la gráfica de la función (x = – 4 es un valor admitido en este intervalo), por lo tanto dicho punto se ilustra como ●, mientras que el punto ( – 3 , – 4) no pertenece a la gráfica en este intervalo (x < – 3), por lo tanto dicho punto si ilustra como ○.
Sea n = – 3. De acuerdo con la definición de la función parte entera:
f (x) = – 3 si – 3 ≤ x < – 3 + 1
si – 3 ≤ x < – 2
Esto se interpreta diciendo que si – 3 ≤ x < – 2, entonces f (x) es una función constante, f (x) = – 3. La gráfica es una recta horizontal.
La gráfica de la función f (x) = ⟦ x ⟧ en el intervalo – 3 ≤ x < – 2 es:

Obsérvese que el punto ( – 3 , – 3 ) pertenece a la gráfica de la función (x = – 3 es un valor admitido en este intervalo), por lo tanto dicho punto se ilustra como ●, mientras que el punto ( – 2 , – 3) no pertenece a la gráfica en este intervalo (x < – 2), por lo tanto dicho punto si ilustra como ○.
Sea n = 4. De acuerdo con la definición de la función parte entera:
f (x) = 3 si 3 ≤ x < 3 + 1
si 3 ≤ x < 4
Esto se interpreta diciendo que si 3 ≤ x < 4, entonces f (x) es una función constante, f (x) = 3. La gráfica es una recta horizontal.
La gráfica de la función f (x) = ⟦ x ⟧ en el intervalo 3 ≤ x < 4 es:
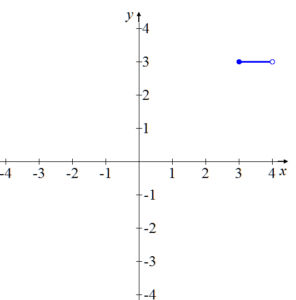
Obsérvese que el punto ( 3 , 3 ) pertenece a la gráfica de la función (x = 3 es un valor admitido en este intervalo), por lo tanto dicho punto se ilustra como ●, mientras que el punto ( 4 , 3) no pertenece a la gráfica en este intervalo (x < 4), por lo tanto dicho punto si ilustra como ○.
A continuación se muestra un resumen de los valores asignados a n y el intervalo de aplicación en x para la función parte entera.
|
n |
Inecuación |
Intervalo Sol. x |
f (x) = ⟦ x ⟧ |
|
– 4 |
(– 4) ≤ x < (– 4) + 1 |
– 4 ≤ x < – 3 |
– 4 |
|
– 3 |
(– 3) ≤ x < (– 3) + 1 |
– 3 ≤ x < – 2 |
– 3 |
|
– 2 |
(– 2) ≤ x < (– 2) + 1 |
– 2 ≤ x < – 1 |
– 2 |
|
– 1 |
(– 1) ≤ x < (– 1) + 1 |
– 1 ≤ x < 0 |
– 1 |
|
0 |
(0) ≤ x < (0) + 1 |
0 ≤ x < 1 |
0 |
|
1 |
(1) ≤ x < (1) + 1 |
1 ≤ x < 2 |
1 |
|
2 |
(2) ≤ x < (2) + 1 |
2 ≤ x < 3 |
2 |
|
3 |
(3) ≤ x < (3) + 1 |
3 ≤ x < 4 |
3 |
A continuación se muestra la gráfica de la función parte entera.

Comúnmente para hallar el valor de la función en un punto o en un intervalo se asignan valores a x y se determina el valor de la función. En el caso de la función parte entera este procedimiento se invierte, esto es, se asigna un valor (entero) a la función y se determina el intervalo de valores de x en los cuales la función adopta ese valor asignado.
Rango de la función parte entera.
Rgo f = { … , – 5 , – 4 , – 3 , – 2 , – 1 , 0 , 1 , 2 , 3 , 4 , 5 , …} = ℕ (El conjunto de los números naturales).
Valoraciones
No hay valoraciones aún.