Descripción
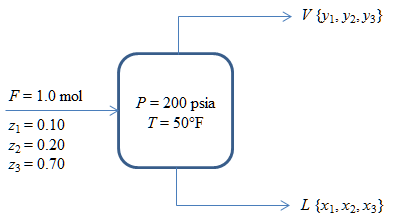
Una mezcla líquida de los hidrocarburos: metano (1), etano (2) y propano (3) se envía a un separador a 50°F y 200 lb/plg2 a través de una válvula reguladora, donde sufre una vaporización instantánea. ¿Cuál es la fracción de la corriente alimentada que sale del separador en fase líquida y cuáles son las composiciones de las fases de equilibrio? Las composiciones de la alimentación son: z1 = 0.10, z2 = 0.20, z3 = 0.70 y los valores de K están dados por las figuras de DePriester.
Referencias:
Ejemplo 8-4 del Smith – Van Ness. Tercera Edición. Página 352.
Ejemplo 14.4 del Smith – Van Ness. Cuarta Edición. Página 501.
Ejemplo 13.4 del Smith – Van Ness. Quinta Edición. Página 568.
Ejemplo 10.6 del Smith – Van Ness. Sexta Edición. Página 390.
Ejemplo 10.6 del Smith – Van Ness. Séptima Edición. Página 358.
Solución.
Componentes: Metano (1); Etano (2); Propano (3)
Temperatura: T = 50°F
Presión: P = 200 lbs/plg2abs
L = ?; xi = ?; yi = ?
Composición de la alimentación: z1 = 0.10, z2 = 0.20, z3 = 0.70
Para averiguar el estado termodinámico de la mezcla se aplica el siguiente criterio:
Utilizar f (V) como indicador preciso.
\( \displaystyle f\,(V)=\sum\frac{Z_i\,(K_i-1)}{1+V\,(K_i-1)}\)
Si f (0) < 0 → Líquido sub-enfriado.
Si f (0) = 0 → Líquido en su Punto de Burbuja.
Si f (1) = 0 → Vapor en su Punto de Rocío.
Si f (1) > 0 → Vapor sobrecalentado.
Si no se cumple alguna de estas condiciones, la corriente será una mezcla de líquido saturado + vapor saturado (Coexistencia de ambas fases en equilibrio).
A P = 200 psia y T = 50°F, de los diagramas de DePriester:

K1 = 10; K2 = 1.76; K3 = 0.52.
\( \displaystyle f\,(V)=\sum\frac{z_i\,(K_i-1)}{1+V\,(K_i-1)}\)
Para una mezcla de tres componentes:
\( \displaystyle f\,(V)=\frac{z_1\,(K_1-1)}{1+V\,(K_1-1)}+\frac{z_2\,(K_2-1)}{1+V\,(K_2-1)}+\frac{z_3\,(K_3-1)}{1+V\,(K_3-1)}\)
\( \displaystyle f\,(V)=\frac{0.10\,(10-1)}{1+V\,(10-1)}+\frac{0.20\,(1.76-1)}{1+V\,(1.76-1)}+\frac{0.70\,(0.52-1)}{1+V\,(0.52-1)}\)
\( \displaystyle f\,(V)=\frac{0.9}{1+9\,V}+\frac{0.152}{1+0.76\,V}+\frac{0.336}{1-0.48\,V}\)
Evaluación de las condiciones límite:
f (0) = 0.9 + 0.152 – 0.336 = 0.716 > 0 → Criterio no concluyente.
\( \displaystyle f\,(1)=\frac{0.9}{1+9}+\frac{0.152}{1+0.76}+\frac{0.336}{1-0.48}\)
\( \displaystyle f\,(1)=\frac{0.9}{10}+\frac{0.152}{1.76}-\frac{0.336}{0.52}\)
f (1) = 0.09 + 0.0864 – 0.6462 = – 0.4698 < 0 → Criterio no concluyente.
Se trata de una mezcla saturada de líquido + vapor en equilibrio.
Cálculo de la fracción de vapor.
f (V) = 0
\( \displaystyle \frac{0.9}{1+9\,V}+\frac{0.152}{1+0.76\,V}-\frac{0.336}{1-0.48\,V}=0\)
Al resolver la ecuación anterior se obtiene: V = 0.2725, por lo tanto, la cantidad relativa de líquido que sale del separador es:
L = 1 – V
L = 1 – 0.2725
L = 0.7275
Cálculo de las composiciones del líquido y el vapor.
Líquido: \( \displaystyle x_i=\frac{z_i}{1+V\,(K_i-1)}\)
\( \displaystyle x_1=\frac{z_1}{1+V\,(K_1-1)}=\frac{0.10}{1+0.2725\,(10-1)}=0.028956\)
\( \displaystyle x_2=\frac{z_2}{1+V\,(K_2-1)}=\frac{0.20}{1+0.2725\,(1.76-1)}=0.165686\)
\( \displaystyle x_3=\frac{z_3}{1+V\,(K_3-1)}=\frac{0.70}{1+0.2725\,(0.52-1)}=0.805338\)
Vapor: yi = Ki xi
y1 = K1 x1 = 10×0.028965 = 0.289650
y2 = K2 x2 = 1.76×0.165686 = 0.291607
y3 = K3 x3 = 0.52×0.805338 = 0.418776
Resumen:
Fracción de líquido: L = 0.7275 (72.75%).
Composición de las fases en equilibrio:
Líquido: x1 = 0.028965; x2 = 0.165686; x3 = 0.805338.
Vapor: y1 = 0.289650; y2 = 0.291607; y3 = 0.418776.
Aplicación del Método de Newton para el cálculo de la fracción de vapor.
a) V1 = 0.5
b) \( \displaystyle f\,(V)=\sum\frac{Z_i\,(K_i-1)}{1+V\,(K_i-1)}\)
\( \displaystyle f\,(V)=\frac{0.9}{1+9\,V}+\frac{0.152}{1+0.76\,V}+\frac{0.336}{1-0.48\,V}\)
\( \displaystyle f\,(0.5)=\frac{0.9}{1+9\,(0.5)}+\frac{0.152}{1+0.76\,(0.5)}+\frac{0.336}{1-0.48\,(0.5)}\)
f (0.5) = 0.163636 + 0.110145 + (– 0.442105)
f (0.5) = – 0.168324
c) \( \displaystyle f´\,(V)=-\sum\frac{z_i\,(K_i-1)^2}{[1+V\,(K_i-1)]^2}\)
\( \displaystyle f´\,(0.5)=-\frac{(0.163636)^2}{0.10}-\frac{(0.110145)^2}{0.20}-\frac{(-0.442105)^2}{0.70}\)
f ´(0.5) = – 0.267769 – 0.060660 – 0.279224
f ´(0.5) = – 0.607653
d) \( \displaystyle V_2=V_1-\frac{f\,(V_1)}{f´\,(V_1)}\)
\( \displaystyle V_2=0.5-\frac{-0.168324}{-0.607653}\)
V2 = 0.5 – 0.2770
V2 = 0.2230
Las iteraciones siguientes se resumen en la tabla mostrada a continuación:
|
Iteración |
f (V) | f ´(V) | V |
|
1 |
0.168324 |
–0.607651 |
0.2230 |
|
2 |
0.052997 |
–1.182542 |
0.2678 |
|
3 |
0.004647 |
–0.988628 |
0.2725 |
|
4 |
0.000041 |
–0.972297 |
0.2725 |
Solución: V = 0.2725 moles.

Valoraciones
No hay valoraciones aún.