Descripción
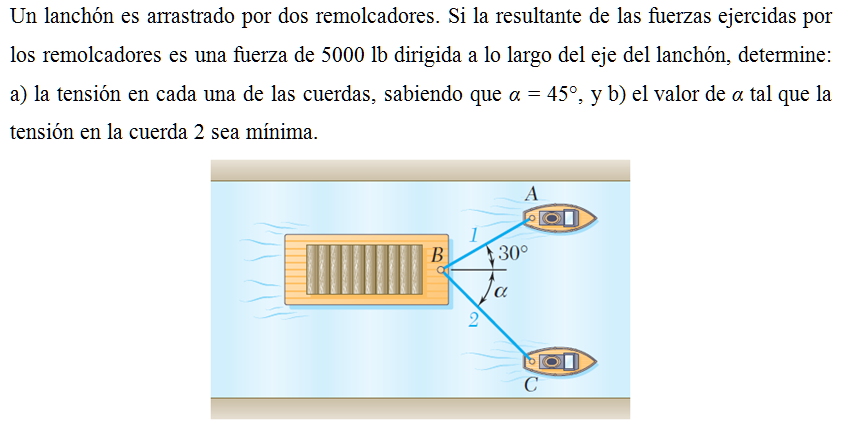
Un lanchón es arrastrado por dos remolcadores. Si la resultante de las fuerzas ejercidas por los remolcadores es una fuerza de 5000 lb dirigida a lo largo del eje del lanchón, determine: a) la tensión en cada una de las cuerdas, sabiendo que α = 45º, y b) el valor de α tal que la tensión en la cuerda 2 sea mínima.
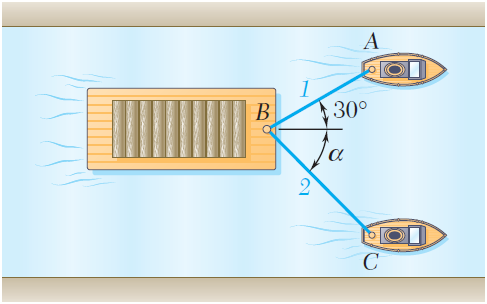
A barge is pulled by two tugboats. If the resultant of the forces exerted by the tugboats is a 5000-lb force directed along the axis of the barge, determine a) the tension in each of the ropes knowing that α = 45°, b) the value of α for which the tension in rope 2 is minimum.
Referencias:
Problema Resuelto 2.2 del Beer – Johnston. Séptima Edición. Página 23.
Problema Resuelto 2.2 del Beer – Johnston. Octava Edición. Página 23.
Problema Resuelto 2.2 del Beer – Johnston. Novena Edición. Página 23.
Sample Problema 2.2 from Beer – Johnston. Ninth Edition. Page 23.
Problema Resuelto 2.2 del Beer – Johnston. Décima Edición. Página 19.
Solución.
a) El diagrama vectorial se muestra a continuación.

Cálculo de θ.
α + 30° + θ = 180°
θ = 180º – α – 30°
θ = 180° – 45° – 30°
θ = 105°
Cálculo de T1.
Teorema del seno.
\( \displaystyle \frac{T_1}{\sin\alpha}=\frac{R}{\sin\theta}\)
\( \displaystyle T_1=\frac{R}{\sin\theta}\times\sin\alpha\)
\( \displaystyle T_1=\frac{5000}{\sin105º}\times\sin45º\)
T1 = 3660.25 lb
Cálculo de T2.
Teorema del seno.
\( \displaystyle \frac{T_2}{\sin30º}=\frac{R}{\sin\theta}\)
\( \displaystyle T_2=\frac{R}{\sin\theta}\times\sin30º\)
\( \displaystyle T_2=\frac{5000}{\sin105º}\times\sin30º\)
T2 = 2588.19 lb
b) Para que T2 sea mínima, debe ser ortogonal a T1.
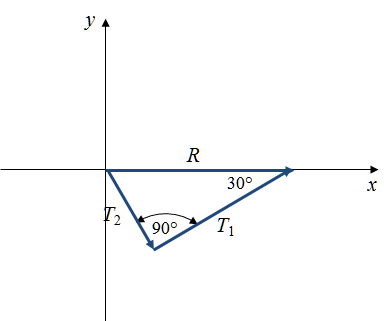
Los valores correspondientes de T1 y T2 son:
T1 = R cos 30°
T1 = 500 cos 30°
T1 = 4330.13 lb
T2 = R sen 30°
T2 = 500 sen 30°
T2 = 250 lb



Valoraciones
No hay valoraciones aún.