Descripción
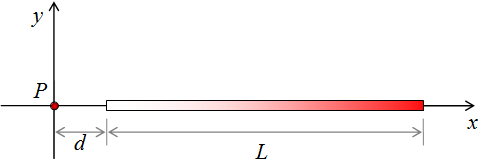
Barra con carga no uniforme. Una línea de carga de longitud L y orientada a lo largo del eje x como en la figura tiene una carga por unidad de longitud que varía como \( \displaystyle \lambda = \frac{\lambda_0\,(x-d)}{d}\), donde d es la distancia de la barra al origen (punto P en la figura) y λ0 una constante. Encuentre el campo eléctrico en el origen. (Sugerencia: un elemento infinitesimal tiene una carga d q = λ d x, pero observe que λ no es una constante.)
Referencias:
Ejemplo 2.4 del Córdova. Página 49.
Problema 68. Capítulo 23 del Serway. Tercera Edición.
Página 33. Problema PP-2.02 del Figueroa. Página 65.
SOLUCIÓN DEL EJERCICIO.
Se considera un elemento diferencial de carga (d q) sobre la barra a una distancia x con respecto al eje y. La influencia que ejerce dicho elemento sobre la carga de prueba colocada en el origen es de repulsión, con un diferencial de campo eléctrico d E (orientado hacia la parte negativa del eje x).
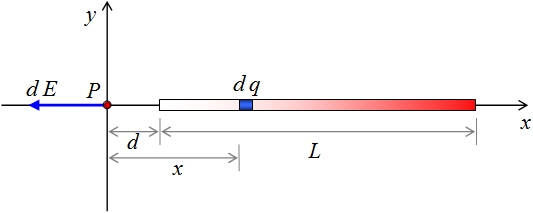
El diferencial del campo eléctrico viene dado por:
\( \displaystyle d\,E = k\frac{d\,q}{r^2}\) (1)
Al integrar ambos miembros de la ecuación (1):
\( \displaystyle \int d\,E=\int k\frac{d\,q}{r^2}\)
\( \displaystyle E=k\int \frac{d\,q}{r^2}\) (2)
Para determinar el diferencial de carga, recurrimos a la definición de densidad lineal de carga:
\( \displaystyle \lambda=\frac{q}{x}\)
Al despejar la carga:
q = λ x
Al diferenciar con respecto a la longitud x:
d q = λ d x (3)
La densidad lineal de carga está dada por:
\( \displaystyle \lambda = \frac{\lambda_0\,(x-d)}{d}\) (4)
Al sustituir la ecuación (4) en la ecuación (3):
\( \displaystyle d\,q = \frac{\lambda_0\,(x-d)}{d}d\,x\) (5)
Distancia entre el elemento diferencial de carga (d q) y la carga de prueba ubicada en el punto P.
r = x (6)
Al sustituir las ecuaciones (5) y (6) en la ecuación (2):
\( \displaystyle E=k\int \frac{\frac{\lambda_0\,(x-d)}{d}d\,x}{x^2}\)
\( \displaystyle E=\frac{k\,\lambda_0}{d}\int\frac{(x-d)\,d\,x}{x^2}\)
Límites de integración.
Para hacer el recorrido de la varilla, la posición del elemento diferencial debe variar desde x = d (El extremo izquierdo de la varilla) hasta x = d + L (El extremo derecho de la varilla).
\( \displaystyle E=\frac{k\,\lambda_0}{d}\int_d^{d+L}\frac{(x-d)\,d\,x}{x^2}\)
\( \displaystyle E=\frac{k\,\lambda_0}{d}\int_d^{d+L}\left(\frac{x-d}{x^2}\right)d\,x\)
\( \displaystyle E=\frac{k\,\lambda_0}{d}\int_d^{d+L}\left(\frac{1}{x}-\frac{d}{x^2}\right)d\,x\)
La integración conduce a:
\( \displaystyle E=\frac{k\,\lambda_0}{d}\left[\left(\ln x+\frac{d}{x}\right)\bigg\vert_d^{d+L}\right]\)
Aplicando el teorema fundamental del cálculo:
\( \displaystyle E=\frac{k\,\lambda_0}{d}\left[\left(\ln (d+L)+\frac{d}{d+L}\right)-(\ln d+1)\right]\)
\( \displaystyle E=\frac{k\,\lambda_0}{d}\left[\ln (d+L)+\frac{d}{d+L}-\ln d-1\right]\)
\( \displaystyle E=\frac{k\,\lambda_0}{d}\left[\ln (d+L)-\ln d+\frac{d}{d+L}-1\right]\)
\( \displaystyle E=\frac{k\,\lambda_0}{d}\left[\ln \left(\frac{d+L}{d}\right)+\frac{d-(d+L)}{d+L}\right]\)
\( \displaystyle E=\frac{k\,\lambda_0}{d}\left[\ln \left(\frac{d}{d}+\frac{L}{d}\right)+\frac{d-d-L}{d+L}\right]\)
\( \displaystyle E=\frac{k\,\lambda_0}{d}\left[\ln \left(1+\frac{L}{d}\right)-\frac{L}{d+L}\right]\)
\( \displaystyle \mathbf{E}=-\frac{k\,\lambda_0}{d}\left[\ln \left(1+\frac{L}{d}\right)-\frac{L}{d+L}\right]\mathbf{i}\)
\( \displaystyle \mathbf{E}=\frac{k\,\lambda_0}{d}\left[\frac{L}{d+L}-\ln \left(1+\frac{L}{d}\right)\right]\mathbf{i}\) (7)



Valoraciones
No hay valoraciones aún.