Descripción
Campo eléctrico de un disco con carga uniforme. Un disco de radio R tiene una densidad de carga superficial uniforme σ. Calcule el campo eléctrico en un punto P que se encuentra a lo largo del eje perpendicular central del disco y a una distancia x del centro del disco.
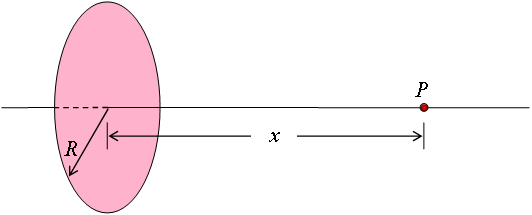
The Electric Field of a Uniformly Charged Disk. A disk of radius R has a uniform surface charge density σ. Calculate the electric field at a point P that lies along the central perpendicular axis of the disk and a distance x from the center of the disk.
Referencias:
Ejemplo 23.8 del Serway. Séptima Edición. Página 658.
Ejemplo 23.10 del Serway. Tercera Edición. Página 17.
SOLUCIÓN DEL EJERCICIO.
Se considera un elemento diferencial de carga (d q) sobre el disco. En este caso es un anillo diferencial. La influencia que ejerce dicho elemento sobre la carga de prueba colocada en el punto P es de repulsión, con un diferencial de campo eléctrico d E (orientado con un ángulo θ respecto a la horizontal). d E se descompone en sus componentes rectangulares d Ex y d Ey.

Componentes rectangulares del campo eléctrico.
Componente horizontal.
\( \displaystyle d\,E_x = d\,E\,\cos\,\theta \) (1)
Componente vertical.
\( \displaystyle d\,E_y = d\,E \sin\,\theta \)
Por simetría Ey = 0
Al integrar ambos miembros de la ecuación (1):
\( \displaystyle \int d\,E_x = \int d\,E\cos\,\theta\)
\( \displaystyle E_x = \int d\,E\cos\,\theta\) (2)
El diferencial del campo eléctrico viene dado por:
\( \displaystyle dE = k\frac{d\,q}{d^2} \) (3)
Al sustituir la ecuación (3) en la ecuación (2):
\( \displaystyle E_x = \int k\frac{d\,q}{d^2}\cos\theta\) (4)
La ecuación (5) puede integrarse en función del radio del elemento diferencial (r) o en función del ángulo (θ).
Primer mecanismo de solución. Cálculo de la integral (4) en función del radio del anillo diferencial.
Para determinar el diferencial de carga, recurrimos a la definición de densidad superficial de carga:
\( \displaystyle \sigma = \frac{q}{A}\)
Al despejar la carga:
q = σ A
Al diferenciar con respecto al área A:
d q = σ d A (5)
Área de un disco:
A = π r2
Al diferenciar con respecto al radio r:
d A = 2 π r d r (6)
Al sustituir la ecuación (6) en la ecuación (5)
d q = σ (2 π r d r)
d q = 2 π σ r d r (7)
Distancia entre el elemento diferencial de carga (d q) y la carga de prueba ubicada en el punto P.
d2 = x2 + r2 (8)
\( \displaystyle d = \sqrt{x^2+r^2} \) (9)
Ángulo que forma el diferencial de campo eléctrico (d E) con la horizontal.
\( \displaystyle cos \theta = \frac{x}{d} \) (10)
Al sustituir la ecuación (9) en la ecuación (10):
\( \displaystyle cos\,\theta = \frac{x}{\sqrt{x^2+r^2}} \) (11)
Al sustituir las ecuaciones (7), (8) y (11) en la ecuación (4):
\( \displaystyle E_x = \int k\frac{2\,\pi\,\sigma\,r\,d\,r}{x^2+r^2}\frac{x}{\sqrt{x^2+r^2}}\)
\( \displaystyle E_x = \int \frac{2\,\pi\,k\,\sigma\,r\,d\,r}{(x^2+r^2)^{\frac{3}{2}}}\)
\( \displaystyle E_x = 2\,\pi\,k\,\sigma\,x\,\int \frac{r\,d\,r}{(x^2+r^2)^{\frac{3}{2}}}\)
Para hacer el barrido del disco, el radio del elemento diferencial debe variar desde r = 0 (El centro del disco) hasta r = R (El radio del disco).
\( \displaystyle E_x = 2\,\pi\,k\,\sigma\,x\,\int_0^R \frac{r\,d\,r}{(x^2+r^2)^{\frac{3}{2}}}\) (12)
La integral se resuelve aplicando cambio de variable:
u2 = x2 + r2
2 u d u = 2 r d r → r d r = u d u
Límites de integración:
Para r = 0: u = x
Para r = R: \( \displaystyle u = \sqrt{x^2+R^2} \)
Al sustituir en la integral:
\( \displaystyle E_x = 2\,\pi\,k\,\sigma\,x \int_x^{\sqrt{x^2+R^2}}\frac{u\,d\,u}{(u^2)^{\frac{3}{2}}}\)
\( \displaystyle E_x = 2\,\pi\,k\,\sigma\,x \int_x^{\sqrt{x^2+R^2}} \frac{u\,d\,u}{u^3}\)
\( \displaystyle E_x = 2\,\pi\,k\,\sigma\,x \int_x^{\sqrt{x^2+R^2}} \frac{d\,u}{u^2}\)
La integración conduce a:
\( \displaystyle E_x = 2\,\pi\,k\,\sigma\,x \left(-\frac{1}{u}\bigg\vert_0^{\sqrt{x^2+R^2}}\right)\)
Aplicando el teorema fundamental del cálculo:
\( \displaystyle E_x = 2\,\pi\,k\,\sigma\,x \left(-\frac{1}{\sqrt{x^2+R^2}}+\frac{1}{x}\right)\)
\( \displaystyle E_x = 2\,\pi\,k\,\sigma\,x \left(\frac{1}{x}-\frac{1}{\sqrt{x^2+R^2}}\right)\)
\( \displaystyle E_x = 2\,\pi\,k\,\sigma \left(1-\frac{x}{\sqrt{x^2+R^2}}\right)\)
\( \displaystyle \mathbf{E} = 2\,\pi\,k\,\sigma \left(1-\frac{x}{\sqrt{x^2+R^2}}\right)\mathbf{i}\) Unidades de campo eléctrico. (13)
Campo eléctrico en función de la carga total del disco.
\( \displaystyle \sigma = \frac{Q}{A}\)
Área del disco: A = π R2
\( \displaystyle \sigma = \frac{Q}{\pi\,R^2}\) (14)
Al sustituir la ecuación (14) en la ecuación (13):
\( \displaystyle \mathbf{E} = 2\,\pi\,k \left(\frac{Q}{\pi\,R^2}\right) \left(1-\frac{x}{\sqrt{x^2+R^2}}\right)\mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left(1-\frac{x}{\sqrt{x^2+R^2}}\right)\mathbf{i}\) Unidades de campo eléctrico. (15)
Segundo mecanismo de solución. Cálculo de la integral (4) en función del ángulo θ.
\( \displaystyle E_x = \int k\frac{d\,q}{d^2}\cos\theta\) (4)
Elemento diferencial de carga.
d q = 2 π σ r d r (6)
De la figura:
\( \displaystyle tan\theta=\frac{r}{x}\)
r = x tan θ (16)
d r = x sec2θ d θ (17)
Al sustituir las ecuaciones (16) y (17) en la ecuación (6):
d q = 2 π σ (x tan θ) (x sec2θ d θ)
d q = 2 π σ x2 tan θ sec2θ d θ (18)
Distancia entre el elemento diferencial de carga (d q) y la carga de prueba ubicada en el punto P.
De la figura:
\( \displaystyle cos\,\theta=\frac{x}{d}\)
\( \displaystyle d=\frac{x}{cos\,\theta}\)
\( \displaystyle d^2=\frac{x^2}{cos^2\theta}\)
d2 = x2sec2θ (19)
Al sustituir las ecuaciones (18) y (19) en la ecuación (4):
\( \displaystyle E_x = \int_0^{\theta_0} k\frac{2\,\pi\,\sigma\,x^2\tan\theta\sec^2\theta d\,\theta}{x^2\sec^2\theta}\cos\,\theta\)
\( \displaystyle E_x = \int_0^{\theta_0} 2\,\pi\,k\,\sigma \tan\,\theta\,d \,\theta\cos\,\theta\)
\( \displaystyle E_x = \int_0^{\theta_0} 2\,\pi\,k\,\sigma\,\sin\,\theta\,d\,\theta\)
La integración donduce a:
\( \displaystyle E_x = -2\,\pi\,k\,\sigma\,\cos\,\theta\,\bigg\vert_0^{\theta_0}\)
Aplicando el teorema fundamental del cálculo:
\( \displaystyle E_x = -2\,\pi\,k\,\sigma\,\cos\,\theta_0 + 2\,\pi\,k\,\sigma\,\cos\,0\)
\( \displaystyle E_x = -2\,\pi\,k\,\sigma\,\cos\,\theta_0 + 2\,\pi\,k\,\sigma\)
\( \displaystyle E_x = 2\,\pi\,k\,\sigma (1-\cos\,\theta_0)\) (20)
De la figura:
\( \displaystyle \cos\theta = \frac{x}{\sqrt{x^2+R^2}}\) (21)
Al sustituir la ecuación (21) en la ecuación (20):
\( \displaystyle E_x = 2\,\pi\,k\,\sigma \left(1-\frac{x}{\sqrt{x^2+R^2}}\right)\)
\( \displaystyle \mathbf{E} = 2\,\pi\,k\,\sigma\,\left(1-\frac{x}{\sqrt{x^2+R^2}}\right)\mathbf{i}\) Unidades de campo eléctrico. (13)
Puede demostrarse que la obtención del campo eléctrico usando el segundo mecanismo de solución se corresponde a la solución de la integral del primer mecanismo mediante una sustitución trigonométrica. Es por ello que se recomienda obtener la expresión (4) (en función de r), y luego evaluar la resolución de la integral mediante un cambio de variables (si aplica), una sustitución trigonométrica o mediante el uso de una tabla de integrales. Obviamente la forma más conveniente de las tres indicadas es mediante una tabla de integrales, sin embargo, esta decisión está sometida a la consideración del Profesor, quien debe indicarlo oportunamente.
Aplicaciones de la ecuación del campo eléctrico para un disco.
Lámina infinita (R → ∞).
\( \displaystyle \mathbf{E} = 2\,\pi\,k\,\sigma \left(1-\frac{x}{\sqrt{x^2+R^2}}\right)\mathbf{i}\) (13)
E = 2 π k σ i
\( \displaystyle k = \frac{1}{4\,\pi\,\epsilon_0}\)
\( \displaystyle \mathbf{E} = 2\,\pi \left(\frac{1}{4\,\pi\,\epsilon_0}\right)\sigma\,\mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{\sigma}{2\,\epsilon_0} \mathbf{i}\) Unidades de campo eléctrico. (22)
Campo eléctrico en un punto “alejado” del centro del disco (x >> R).
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left(1-\frac{x}{\sqrt{x^2+R^2}}\right)\mathbf{i}\) (15)
Se reescribe la expresión del campo eléctrico y se introduce una aproximación.
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left(1-\frac{1}{\frac{\sqrt{x^2+R^2}}{x}}\right)\mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left(1-\frac{1}{\frac{\sqrt{x^2+R^2}}{\sqrt{x^2}}}\right)\mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left(1-\frac{1}{\sqrt{\frac{x^2+R^2}{x^2}}}\right)\mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left(1-\frac{1}{\sqrt{\frac{x^2}{x^2}+\frac{R^2}{x^2}}}\right)\mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left[1-\frac{1}{\sqrt{1+\left(\frac{R}{x}\right)^2}}\right]\mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2}\left[1-
\frac{1}{\left[1+\left(\frac{R}{x}\right)^2\right]^\frac{1}{2}}\right] \mathbf{i}\)
Aplicando la aproximación \( \displaystyle \frac{1}{(1+\delta)^k}=1-k\,\delta\) con \( \displaystyle \delta=\left(\frac{R}{x}\right)^2\) y \( \displaystyle k=\frac{1}{2}\):
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2}\left[1-\left[1-\frac{1}{2}\left(\frac{R}{x}\right)^2\right]\right] \mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2}\left[1-1+\frac{1}{2}\left(\frac{R}{x}\right)^2\right] \mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2}\left[\frac{1}{2}\left(\frac{R}{x}\right)^2\right] \mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2}\left[\frac{1}{2}\left(\frac{R^2}{x^2}\right)\right] \mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2}\left(\frac{R^2}{2\,x^2}\right) \mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{k\,Q}{x^2}\mathbf{i}\)
\( \displaystyle \Vert \mathbf{E} \Vert = \frac{k\,Q}{x^2}\)
El campo eléctrico obtenido es el equivalente al campo eléctrico debido a una carga puntual cuyo valor es Q a una distancia x, esto es, el disco se comporta como una carga puntual.
Forma alterna de reducir la ecuación \( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left(1-\frac{x}{\sqrt{x^2+R^2}}\right)\mathbf{i}\) a la correspondiente a una carga puntual para x >> R.
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left(1-\frac{x}{\sqrt{x^2+R^2}}\right)\mathbf{i}\) (15)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left(\frac{\sqrt{x^2+R^2}-x}{\sqrt{x^2+R^2}}\right)\mathbf{i}\)
Se aplica la conjugada del numerador.
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \cdot\frac{\sqrt{x^2+R^2}-x}{\sqrt{x^2+R^2}}\cdot\frac{\sqrt{x^2+R^2}+x}{\sqrt{x^2+R^2}+x}\,\mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left[\frac{(\sqrt{x^2+R^2}-x)\,(\sqrt{x^2+R^2}+x)}{\sqrt{x^2+R^2}\,(\sqrt{x^2+R^2}+x)}\right]\mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left[\frac{x^2+R^2-x^2}{\sqrt{x^2+R^2}\,(\sqrt{x^2+R^2}+x)}\right]\mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,Q}{R^2} \left[\frac{R^2}{\sqrt{x^2+R^2}\,(\sqrt{x^2+R^2}+x)}\right]\mathbf{i}\)
\( \displaystyle \mathbf{E} = 2\,k\,Q \left[\frac{1}{\sqrt{x^2+R^2}\,(\sqrt{x^2+R^2}+x)}\right]\mathbf{i}\)
x >> R → x2 + R2 ≈ x2
\( \displaystyle \mathbf{E} = 2\,k\,Q \left[\frac{1}{\sqrt{x^2}\,(\sqrt{x^2}+x)}\right]\mathbf{i}\)
\( \displaystyle \mathbf{E} = 2\,k\,Q \left[\frac{1}{x\,(x+x)}\right]\mathbf{i}\)
\( \displaystyle \mathbf{E} = 2\,k\,Q \left[\frac{1}{x\,(2\,x)}\right]\mathbf{i}\)
\( \displaystyle \mathbf{E} = 2\,k\,Q \left(\frac{1}{2\,x^2}\right)\mathbf{i}\)
\( \displaystyle \mathbf{E} = \frac{k\,Q}{x^2}\mathbf{i}\) Unidades de campo eléctrico.


Valoraciones
No hay valoraciones aún.