Descripción

Densidad de carga volumétrica.

La densidad de carga volumétrica se define por:

\( \displaystyle \rho = \frac {q}{V} \)

ρ es la densidad de carga volumétrica.

q es la carga distribuida en el sólido.

V es el volumen del sólido.

La densidad de carga volumétrica es aplicable a cilindros y esferas.

\( \displaystyle q = \int_{r_0}^{r_1} \rho\,(r)\,d\,V \)

q es la carga del cilindro o de la esfera.

ρ (r) es la densidad de carga volumétrica del cilindro o de la esfera.

r₀ y r₁ son los límites de la sección del cilindro o la esfera en la cual se determina la carga.

Cilindros.

Para un cilindro de radio R y longitud L.

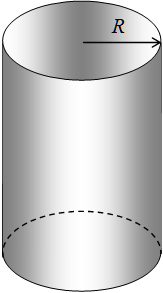
\( \displaystyle q = \int_{r_0}^{r_1} \rho\,(r)\,d\,V \)

Volumen de un elemento diferencial del cilindro.

V = π r² L

d V = 2 π r L d r

\( \displaystyle q = \int_{r_0}^{r_1} \rho\,(r)\,(2\,\pi\,r\,L\,d\,r) \)

Si la densidad de carga volumétrica es constante, la carga se determina mediante la ecuación q = ρ V, teniéndose los dos casos siguientes:

a) r < R.

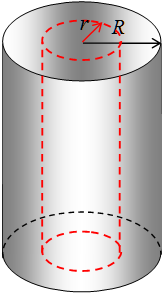
El volumen es V = π r² L y q = π ρ r² L. La carga interna depende del radio considerado.

b) r ≥ R.

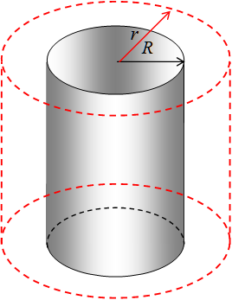
El volumen es V = π R² L y q = π ρ R² L, la carga interna no depende del radio considerado.