Descripción

Una de las partes más importantes de la geometría analítica es la construcción de figuras a partir de sus ecuaciones. La construcción de un plano se facilita considerablemente por la determinación de sus intersecciones con los ejes coordenados y con los planos coordenados.

Intersecciones de un plano con los ejes coordenados.

La intersección de un plano con un eje coordenado es la coordenada correspondiente del punto de intersección del plano y el eje coordenado.

Para determinar la intersección del plano a x + b y + c z + d = 0 con los ejes coordenados (x , y y z) aplicaremos lo siguiente:

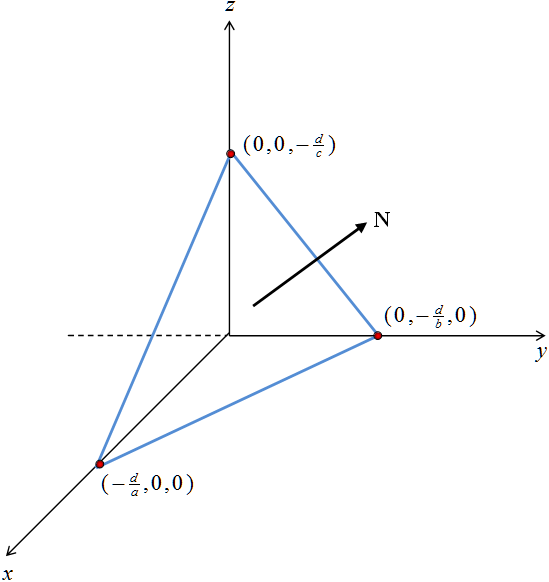
– Intersección con el eje x: Sustituir y = 0 y z = 0 en la ecuación del plano y resolver en x la ecuación de primer grados resultante. El punto obtenido es \( \displaystyle \left(-\frac{d}{a},0,0\right)\).

– Intersección con el eje y: Sustituir x = 0 y z = 0 en la ecuación del plano y resolver en y la ecuación de primer grado resultante. El punto obtenido es \( \displaystyle \left(0,-\frac{d}{b},0\right)\).

– Intersección con el eje z: Sustituir x = 0 y y = 0 en la ecuación del plano y resolver en z la ecuación de primer grado resultante. El punto obtenido es \( \displaystyle \left(0,0,-\frac{d}{c}\right)\).

Intersecciones de un plano con los planos coordenados.

La traza de un plano sobre un plano coordenado es la recta de intersección del plano y el plano coordenado.

Para determinar las trazas del plano con los planos coordenados (x y, x z y y z) aplicaremos lo siguiente:

– Trazas sobre el plano x y: Sustituir z = 0 en la ecuación del plano y obtener la ecuación de la recta en el plano x y. La recta obtenida es a x + b y + d = 0.

– Trazas sobre el plano x z: Sustituir y = 0 en la ecuación del plano y obtener la ecuación de la recta en el plano x z. La recta obtenida es a x + c z + d = 0.

– Trazas sobre el plano y z: Sustituir x = 0 en la ecuación del plano y obtener la ecuación de la recta en el plano y z. La recta obtenida es b y + c z + d = 0.

Una forma útil de la ecuación del plano que permite determinar las intersecciones con los ejes y las trazas sobre los planos coordenados es la ecuación simétrica del plano.