Descripción
Si a, b y c son no nulos y son la intersección de los ejes x, y, z respectivamente de un plano, demuestre que una ecuación del plano es \( \displaystyle \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\).
Referencia: Guía de Ejercicios Prof. Eulogio Herrera. Universidad de Oriente. Núcleo de Anzoátegui. Abril 2025.
Solución.
Para determinar la ecuación de un plano, se deben conocer un punto perteneciente al plano y el vector normal del mismo.
La ecuación canónica del plano buscado es:
Nx (x – x0) + Ny (y – y0) + Nz (z – z0) = 0 (1)
Siendo x0 , y0, z0 las coordenadas de un punto del plano y Nx, Ny y Nz las componentes a lo largo de los ejes x, y y z, respectivamente.
Punto perteneciente al plano.
Puesto que se conoce la intersección del plano con cada uno de los ejes coordenados, se dispone de los puntos siguientes:
Corte con el eje x: (a , 0 , 0)
Corte con el eje y: (0 , b , 0)
Corte con el eje z: (0 , 0 , c)
Esto significa que disponemos de tres puntos. Cualquiera de estos tres puntos puede ser utilizado para determinar la ecuación del plano. Elegiremos el punto ( x0 , y0 , z0 ) = (a , 0 , 0), de donde resulta:
x0 = a
y0 = 0
z0 = 0 (2)
Independientemente del punto que elijamos, vamos a encontrar la misma ecuación para el plano buscado.
Vector normal del plano buscado.
Dado que se conocen tres puntos del plano, podemos definir un par de vectores entre ellos, asegurándonos de utilizar los tres puntos. Siendo los puntos conocidos: A (a , 0 , 0), B (0 , b , 0) y C (0 , 0 , c), un par de vectores pueden ser:
AB = – a i + b j + 0 k
AC = – a i + 0 j + c k
Ambos vectores están sobre el plano, de tal manera que su producto vectorial genera un vector normal a ambos y por lo tanto, normal al plano. El vector normal del plano es:
N = AB × AC
\( \displaystyle \mathbf{N}=\begin{vmatrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\-a&b&0\\-a&0&c\end{vmatrix}
\)
Se duplican la primera y segunda columnas del determinante:
\( \displaystyle \mathbf{N}=\begin{vmatrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\-a&b&0\\-a&0&c\end{vmatrix}\begin{array}&\mathbf{i}&\mathbf{j}\\-a&b\\-a&0\end{array}\)
N = (b c i) – (–a b k – a c j)
N = b c i + a c j + a b k
Se tiene entonces que las componentes del vector normal son:
Nx = b c
Ny = a c
Nz = a b (3)
Al sustituir las coordenadas del punto ( x0 , y0 , z0 ) seleccionado (Ecuaciones 2) y las componentes del vector normal (Ecuaciones 3) en la ecuación del plano buscado (Ecuación 1):
b c (x – a) + a c (y – 0) + a b (z – 0) = 0
Al aplicar propiedad distributiva:
b c x – a b c + a c y + a b z = 0
b c x + a c y + a b z = a b c
Al dividir la ecuación anterior entre a b c:
\( \displaystyle \frac{b\,c\,x+a\,c\,y+a\,b\,c+a\,b\,z}{a\,b\,c}=\frac{a\,b\,c}{a\,b\,c}\)
Se separan los términos en el miembro izquierdo de la ecuación anterior:
\( \displaystyle \frac{b\,c\,x}{a\,b\,c}+\frac{a\,c\,y}{a\,b\,c}+\frac{a\,b\,z}{a\,b\,c}=1\)
Al simplificar factores en los tres primeros términos:
\( \displaystyle \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
La anterior es la ecuación del plano que satisface las condiciones dadas en el planteamiento del problema.
Nota del autor.
Se evitó utilizar la forma generalizada a (x – x0) + b (y – y0) + c (z – z0) = 0 porque a, b y c son parámetros involucrados en el planteamiento del problema y no coinciden con las componentes del vector normal del plano buscado.
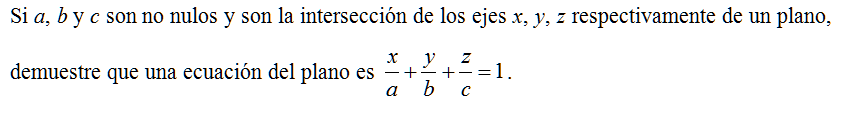


Valoraciones
No hay valoraciones aún.