Descripción
La ecuación de un plano es 4 x + 6 y + 3 z – 12 = 0. Hallar sus intersecciones con los ejes coordenados y las ecuaciones de sus trazas sobre los planos coordenados.
Referencia: Ejemplo 2. Sección 116 del Lehmann. Página 346.
Solución.
Ecuación del plano:
4 x + 6 y + 3 z – 12 = 0
Intersección del plano con los ejes coordenados.
Eje x: y = 0, z = 0. Al sustituir en la ecuación del plano:
4 x + 6 (0) + 3 (0) – 12 = 0
4 x – 12 = 0
x = 3
El punto de intersección del plano con el eje x es: ( 3 , 0 , 0 ).
Eje y: x = 0, z = 0. Al sustituir en la ecuación del plano:
4 (0) + 6 y + 3 (0) – 12 = 0
6 y – 12 = 0
y = 2
El punto de intersección del plano con el eje y es: ( 0 , 2 , 0 ).
Eje z: x = 0, y = 0. Al sustituir en la ecuación del plano:
4 (0) + 6 (0) + 3 z – 12 = 0
3 z – 12 = 0
z = 4
El punto de intersección del plano con el eje z es: ( 0 , 0 , 4 ).
Los puntos de intersección del plano 4 x + 6 y + 3 z – 12 = 0 con los ejes x, y y z son
( 3 , 0 , 0 ), ( 0 , 2 , 0 ) y ( 0 , 0 , 4 ) respectivamente.
Trazas del plano sobre los planos coordenados.
Plano xy: z = 0
Al sustituir en la ecuación del plano:
4 x + 6 y + 3 (0) – 12 = 0
4 x + 6 y – 12 = 0
Plano xz: y = 0
Al sustituir en la ecuación del plano:
4 x + 6 (0) + 3 z – 12 = 0
4 x + 3 z – 12 = 0
Plano yz: x = 0
Al sustituir en la ecuación del plano:
4 (0) + 6 y + 3 z – 12 = 0
6 y + 3 z – 12 = 0
Las trazas del plano 4 x + 6 y + 3 z – 12 = 0 sobre los planos coordenados xy , xz y yz son las rectas 4 x + 6 y – 12 = 0, 4 x + 3 z – 12 = 0 y 6 y + 3 z – 12 = 0 respectivamente.
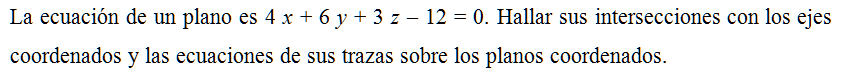


Valoraciones
No hay valoraciones aún.