Descripción
Calcular \( \displaystyle \int\frac{d\,x}{x^2\sqrt{9-x^2}}\).
Referencias:
Ejemplo 1. Sección 10.6 del Larson. Segunda Edición. Página 466.
Ejemplo 1. Sección 8.4 del Larson – Hostetler – Edwards. Octava Edición. Página 544.
Ejemplo 117 del Filippis. Página 291.
Ejemplo 6.5 del Cortés. Octava Edición. Página 169.
Ejemplo 32.12 del Ayres – Mendelson. Quinta Edición. Página 265.
Problema 66. Capítulo 32 del Ayres – Mendelson. Quinta Edición. Página 273.
Solución.
El integrando tiene la forma \( \displaystyle\sqrt{a^2-u^2}\), se hace la sustitución:
| x = 3 sen θ | d x = 3 cos θ d θ | \( \sqrt{9 – x^2} = \sqrt{9 – (3 \sin \theta)^2} \) |
| \(\sqrt{9 – x^2}= \sqrt{9 – 9 \sin^2 \theta} \) | ||
| \(\sqrt{9 – x^2}= \sqrt{9\,(1 – \sin^2 \theta)} \) | ||
| \(\sqrt{9 – x^2}= \sqrt{9 \cos^2 \theta} \) | ||
| \(\sqrt{9 – x^2}= 3 \cos \theta \) |
Al sustituir d x = 3 cos θ d θ, x = 3 sen θ y \( \displaystyle\sqrt{9-x^2}=3\,\cos\theta\) en la integral:
\( \displaystyle \int\frac{d\,x}{x^2\sqrt{9-x^2}}=\int\frac{3\,\cos\theta\,d\,\theta}{(3 \sin \theta)^2\,(3\,\cos\theta)}\)
\( \displaystyle \int\frac{d\,x}{x^2\sqrt{9-x^2}}=\int\frac{3\,\cos\theta\,d\,\theta}{9 \sin^2\theta\cdot 3\,\cos\theta}\)
Al simplificar los valores numéricos el factor cos θ:
\( \displaystyle \int\frac{d\,x}{x^2\sqrt{9-x^2}}=\int\frac{d\,\theta}{9 \sin^2\theta}\)
\( \displaystyle \int\frac{d\,x}{x^2\sqrt{9-x^2}}=\frac{1}{9}\int\frac{d\,\theta}{\sin^2\theta}\)
\( \displaystyle \int\frac{d\,x}{x^2\sqrt{9-x^2}}=\frac{1}{9}\int \csc^2\theta\,d\,\theta\)
La integración conduce a:
\( \displaystyle \int\frac{d\,x}{x^2\sqrt{9-x^2}}=\frac{1}{9} (-\cot\theta)+C\)
\( \displaystyle \int\frac{d\,x}{x^2\sqrt{9-x^2}}=-\frac{1}{9} \cot\theta+C\) (1)
Para volver a la variable original se debe definir cot θ en función de x.
Partiendo de la sustitución trigonométrica realizada:
x = 3 sen θ
\( \displaystyle \sin\theta=\frac{x}{3}=\frac{\text{Cateto opuesto}}{\text{Hipotenusa}}\)
Se construye un triángulo rectángulo cuyo cateto opuesto es x e hipotenusa es 3. El lado faltante, se determina con la aplicación del teorema de Pitágoras.
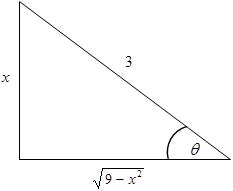
Observe que la magnitud del lado faltante coincide con la expresión \( \displaystyle\sqrt{9-x^2}\) que se encuentra en el integrando.
A partir del triángulo obtenido, se define cot θ.
\( \displaystyle \cot\theta=\frac{\text{Cateto adyacente}}{\text{Cateto opuesto}}\)
\( \displaystyle \cot\theta=\frac{\sqrt{9-x^2}}{x}\) (2)
Al sustituir la ecuación (2) en la ecuación (1):
\( \displaystyle \int\frac{d\,x}{x^2\sqrt{9-x^2}}=-\frac{1}{9}\left(\frac{\sqrt{9-x^2}}{x}\right)+C \)
\( \displaystyle \int\frac{d\,x}{x^2\sqrt{9-x^2}}=-\frac{\sqrt{9-x^2}}{9\,x}+C \)


Valoraciones
No hay valoraciones aún.