Descripción
Preliminares acerca de relaciones y funciones.
Conjunto.
Intuitivamente, un conjunto es una lista o colección de objetos bien definida considerada como un objeto en sí que designaremos con letras mayúsculas A, B, X, Y… Los objetos de la colección pueden ser cualquier cosa: números, colores, letras, figuras, personas, etc. Cada uno de los objetos en la colección es un elemento o miembro del conjunto y los designaremos por letras minúsculas (a menos que dichos elementos sean, a su vez, conjuntos). Si el conjunto A está formado por los elementos a, b y c, escribiremos: A = { a , b , c } y su diagrama de Venn correspondiente será
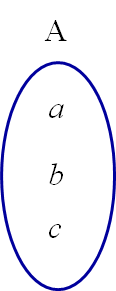
Diagrama de Venn.
Por ejemplo, el conjunto de los colores del arcoíris es:
A = { Rojo , Naranja , Amarillo , Verde , Azul , Añil , Violeta }
Un conjunto suele definirse mediante una propiedad que todos sus elementos poseen. Por ejemplo, para los números naturales, si consideramos la propiedad de ser un número primo, el conjunto de los números primos es:
P = { 2 , 3 , 5 , 7 , 11 , 13 }
La proposición “a ∈ A” se lee “a pertenece a A”, o bien “el elemento a pertenece al conjunto A”. Su negación es “a ∉ A”.
Un conjunto queda definido únicamente por sus miembros y por nada más. En particular el orden en el que se representen estos es irrelevante. Además, cada elemento puede aparecer de manera idéntica una sola vez, esto es, no puede haber elementos totalmente idénticos repetidos. Por ejemplo:
S = { Lunes , Martes , Miércoles , Jueves , Viernes }
S = { Martes , Viernes , Jueves , Lunes , Miércoles }
A = { Rojo , Naranja , Amarillo , Verde , Azul , Añil , Violeta }
A = { Amarillo , Naranja , Rojo , Verde , Violeta , Añil , Azul }
Los conjuntos pueden ser finitos o infinitos. El conjunto de los número naturales es infinito, pero el conjunto de los planetas en el Sistema Solar es finito (tiene ocho elementos). Además, con los conjuntos pueden combinarse mediante operaciones, de manera similar a las operaciones con números.
Los conjuntos son un concepto primitivo, en el sentido de que no es posible definirlos en términos de nociones más elementales, por lo que su estudio puede realizarse de manera informal, apelando a la intuición y a la lógica. Por otro lado, son el concepto fundamental de la matemática: mediante ellos puede formularse el resto de objetos matemáticos, como los números y las funciones, entre otros. Su estudio detallado requiere pues la introducción de axiomas y conduce a la teoría de conjuntos.
Determinación de conjuntos.
Por extensión: cuando se nombran o enumeran todos los elementos que constituyen el conjunto. Por ejemplo:
A = { 1 , 3 , 7 , 10 }, B = { a , e , i , o , u }, C = { Venezuela , Brasil }
Por comprensión: Cuando se da la propiedad que caracteriza los elementos del conjunto. Ejemplo:
A = { x ∈ ℕ / x es par}, B = { x ∈ ℕ / x ≤ 5 },
C = { x ∈ ℝ / x es solución de x2 – 3 x + 2 = 0 }
Conjuntos especiales.
Conjuntos numéricos:
ℕ = { 0 , 1 , 2 , 3 , …} Conjunto de los números naturales.
ℤ Conjunto de los números enteros.
ℚ Conjunto de los números racionales.
I Conjunto de los números irracionales.
ℝ Conjunto de los números reales.
ℂ Conjunto de los números complejos.
ℤ+, ℚ+, I+, ℝ+ Conjunto de los números (enteros, racionales, irracionales, reales) positivos.
ℤ–, ℚ–, I–, ℝ– Conjunto de los números (enteros, racionales, irracionales, reales) negativos.
ℕ*, ℤ*, ℚ*, ℝ*, ℂ* Conjunto de los números (naturales, enteros, racionales, reales, complejos) sin incluir el cero.
Conjunto universal: Depende de lo que se estudie en el momento, es fijado de antemano y está formado por todos los elementos que intervienen en el tema de interés. Se denotará como U.
Conjunto vacío: Es aquel que carece de elementos. Se denotará por ∅.
Conjunto unitario: Formado por un único elemento. Ejemplo: A = { 5 }.
Operaciones con conjuntos.
Unión: La unión de dos conjuntos A y B es el conjunto formado por los elementos que pertenecen a A ó a B. Simbólicamente A ∪ B = { x ∈ U / x ∈ A ∀ x ∈ B }.
Intersección: La intersección de dos conjuntos A y B es el conjunto formado por los elementos que pertenecen a A y a B. Simbólicamente A ∩ B = { x ∈ U / x ∈ A ∧ x ∈ B }.
Diferencia: La diferencia de dos conjuntos A y B es el conjunto formado por los elementos que pertenecen a A y pero que no pertenecen a B. Simbólicamente
A – B = { x ∈ U / x ∈ A ∧ x ∉ B }.
Complemento de un conjunto: Sea A ⊆ U, el complemento de A, que denotaremos por Ac, es el conjunto formado por los elementos de U que no pertenecen a A.
Propiedades de las operaciones con conjuntos.
1. (Ac)c = A
2. A ∪ A = A
3. A ∩ A = A
4. A ∪ B = B ∪ A
5. A ∩ B = B ∩ A
6. A ∪ (B ∪ C) = (A ∪ B) ∪ C
7. A ∩ (B ∩ C) = (A ∩ B) ∩ C
8. A ∪ ∅ = A
9. A ∩ ∅ = ∅
10. A ∪ U = U
11. A ∩ U = A
Par ordenado.
Un par ordenado son dos números que indican valores de dos variables en un orden dado.
Se escribe en la forma ( a , b ), donde a es un elemento perteneciente al conjunto A, y b un elemento perteneciente al conjunto B.
Producto cartesiano.
El producto cartesiano es el conjunto de todos los pares ordenados que pueden formarse tomando como primer elemento un elemento del primer conjunto y como segundo elemento uno del segundo conjunto. Por ejemplo, sean los conjuntos A = { a , b , c } y B = { 1 , 2 }. El producto cartesiano, denotado por A × B viene dado por:
A × B = {( a , 1 ), ( a , 2 ), ( b , 1 ), ( b , 2 ), ( c , 1 ), ( c , 2 )} (1)
Relación.
Cuando se formula una expresión que liga dos o más objetos entre sí, postulamos una relación.
El concepto de relación podría resumirse como la aplicación de una regla que permite vincular un elemento ”x” de un conjunto con uno o varios elementos ”y” de otro conjunto dado mediante algún criterio particular.
El concepto de relación implica la idea de correspondencia entre los elementos de dos conjuntos que forman pares ordenados.
Formalmente, se llama relación a todo subconjunto del conjunto producto cartesiano.
Algunas relaciones que se pueden formar del producto cartesiano (1) son:
R1 = { ( b , 2 ) }
R2 = { ( a , 2 ) , ( c , 1 ) }
R3 = { ( a , 1 ) , ( b , 2 ) , ( c , 1 ) }
R4 = { ( a , 1 ) , ( a , 2 ) , ( b , 2 ) , ( c , 1 ) }
R5 = { ( a , 1 ) , ( a , 2 ) , ( b , 1 ) , ( b , 2 ) , ( c , 1 ) , ( c , 2 ) }
Tipos de relaciones.
En las relaciones se diferencian los tipos según el número de conjuntos en el producto cartesiano, que es el número de términos de la relación:
Relación unaria: un solo conjunto R ⊆ A, R (a)
Relación binaria: con dos conjuntos R ⊆ A1 × A2, R ( a1 , a2 )
Relación ternaria: con tres conjuntos R ⊆ A1 × A2 × A3, R ( a1 , a2 , a3)
Relación cuaternaria: con cuatro conjuntos R ⊆ A1 × A2 × A3 × A4, R ( a1 , a2 , a3 , a4 )
Relación n-aria: caso general con n conjuntos R ⊆ A1 × A2 × … An, R ( a1 , a2 , … an)
Elementos de una relación.
Conjunto de partida.
Es el conjunto cuyos elementos tienen correspondencia en el conjunto de llegada.
Conjunto de llegada.
Es el conjunto cuyos elementos son imagen de los elementos del conjunto de partida.
Dominio.
Es el conjunto formado por los elementos del conjunto de partida que tienen imagen en el conjunto de llegada.
Rango.
Es el conjunto formado por los elementos del conjunto de llegada que son imagen de algún elemento del conjunto de partida.
Valoraciones
No hay valoraciones aún.