Descripción
Funciones ramificadas.
Definición de funciones ramificadas.
Son funciones definidas por intervalos (función definida a trozos), la cual se define empleando más de una expresión o función de las estudiadas anteriormente.
Ejemplos de funciones ramificadas.
Un ejemplo de una función ramificada en la vida cotidiana es el costo de tranporte [C (x), $] según la distancia recorrida (x, km) donde los trayectos cortos tienen tarifa fija mientras que los trayectos largos tienen un recargo lineal en función de la distancia.
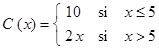
Un ejemplo adicional suele presentarse en el área de ingeniería de petróleo, donde el caudal de producción Q (x) depende de la presión del yacimiento. A baja presión el caudal se mantiene constante por bombeo artificial, a presión media el caudal aumenta linealmente por empuje natural y finalmente a alta presión, el caudal se ajusta con una curva cuadrática que considera efectos no lineales tales como daño de formación o saturación del gas.

Evaluación de funciones ramificadas.
Para evaluar una función ramificada en un punto (x0), el valor de x0 dado debe ubicarse en una de las ramas de la función dependiendo del intervalo de definición de cada una de ellas. Una vez que se identifica la rama, se sustituye el valor de x0 dado, obteniéndose de esta manera la imagen o valor de y correspondiente al valor de x0 dado, esto es, f (x0). Cuando el valor de x0 no se puede ubicar en ninguna de las ramas de la función, se dice que f (x0) no existe.
Dominio de funciones ramificadas.
El dominio de estas funciones ramificadas es la unión del dominio de cada una de las ramas.
Gráfico de funciones ramificadas.
La gráfica de funciones ramificadas se realiza analizando cada una de las ramas de la función en forma independiente. Es necesario identificar el tipo de cada una, y analizarla en el intervalo de aplicación correspondiente. En este punto se resalta la importancia del estudio de funciones con dominio restringido analizado en funciones anteriores.
Puede ocurrir que una rama de la función sea a su vez una función ramificada (valor absoluto de x, signo de x, entre otras), en cuyo caso se debe desglosar la función original en ramificaciones adicionales previo al análisis. Una vez que se analiza cada ramificación en forma individual, se grafican todas en un mismo sistema de coordenadas.
Rango de funciones ramificadas.
El rango en las funciones ramificadas se determina a partir de la gráfica de la función.
Valoraciones
No hay valoraciones aún.