Descripción
Función valor absoluto de x.
Definición de la función valor absoluto.
La función valor absoluto de x, denotada por | x | es una función ramificada definida como:

El valor absoluto se puede definir como \( f\,(x) = \vert x \vert =\sqrt{x^2}\).
| x | se lee “valor absoluto de x”.
El resultado que se obtiene al calcular el valor absoluto de un número es el mismo número con signo positivo. En base a lo anterior:
| | 2 | = 2 | | 4.3 | = 4.3 |
| | 1.999 | = 1.999 | | – 3 | = 3 |
| | – 1.5 | = 1.5 | | – 4.001 | = 4.001 |
| \( \vert \, \frac{3}{4} \, \vert = \frac{3}{4}\) | \( \vert -\frac{7}{3} \, \vert = \frac{7}{3}\) |
| | π | = π | \( \vert \, \sqrt{3} \, \vert = \sqrt{3}\) |
| \( \vert \, 1+\sqrt{5} \, \vert = 1+\sqrt{5}\) | \( \vert \, 3-\sqrt{12} \, \vert = \sqrt{12}-3\) |
| \( \vert -2-\sqrt{7} \, \vert = 2+\sqrt{7}\) | \( \big\vert \, \frac{6-5\,\sqrt{3}}{2} \, \big\vert = \frac{5\,\sqrt{3}-6}{2}\) |
Dominio de la función valor absoluto.
Dom f = ℝ
Gráfico de la función valor absoluto.
La función valor absoluto es una función ramificada, por lo tanto, para construir su gráfica se analiza cada rama por separado.
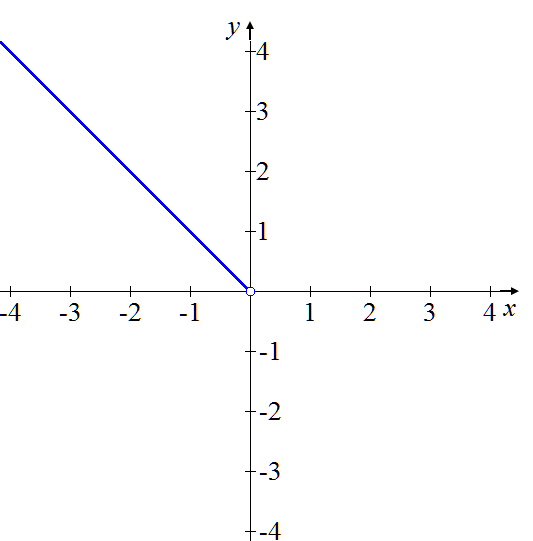
Intervalo x < 0: ( – ∞ , 0 ):
f (x) = – x (Función lineal con pendiente negativa).
Dándole valores a x en el intervalo en estudio:
| x | f (x) = – x |
|
–3 |
– (–3) = 3 |
|
–2 |
– (–2) = 2 |
|
–1 |
– (–1) = 1 |
|
0 |
– (0) = 0 |
Obsérvese que el punto ( 0 , 0 ) no pertenece a la gráfica de esta rama de la función (x < 0), por lo tanto dicho punto se ilustra como ○.
Intervalo x ≥ 0: [ 0 , + ∞ ):
f (x) = x (Función lineal con pendiente positiva).
Dándole valores a x en el intervalo en estudio:
| x | f (x) = x |
|
0 |
0 |
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |

Obsérvese que el punto ( 0 , 0 ) pertenece a la gráfica de esta rama de la función (x = 0 es un valor admitido en este intervalo), por lo tanto dicho punto se ilustra como ●.
Una vez analizada cada rama, se obtiene la gráfica siguiente para la función f (x) = | x |.
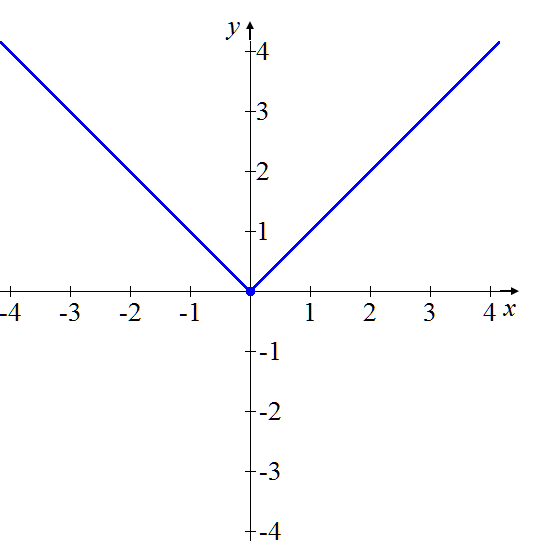
Función valor absoluto de x.
Rango de la función valor absoluto.
El rango está formado por los números reales mayores o iguales a cero.
Rgo f = [ 0 , + ∞ )
Comentario del autor.
Dada una expresión P (x), si definimos una función como f (x) = | P (x) |, la gráfica de la función es la rectificación de la gráfica de P (x), esto es, las partes positivas de la gráfica (por encima del eje de las x) de P (x) permanecen iguales, mientras que las partes negativas (por debajo del eje de las x) se convierten en positivas. Los ceros en la función P (x) permanecen iguales en la función f (x) = | P (x) |. En los ejemplos siguientes se ilustran estas situaciones.
Ejemplo ilustrativo 1.
Si tenemos la función f (x) = x – 3, su gráfica se muestra a continuación.

f (x) = x – 3
Discriminemos la parte positiva de la función (azul), la cual se encuentra por encima del eje x y la negativa (roja), que se encuentra por debajo del eje x.

Para obtener la gráfica de la función valor absoluto correspondiente a la función f (x) = x – 3, esto es, f (x) = | x – 3 |, las partes positivas de la gráfica (azul) permanecen iguales y las negativas se reflejan sobre el eje x. El cero permanece igual en ambas. Se obtiene lo siguiente:
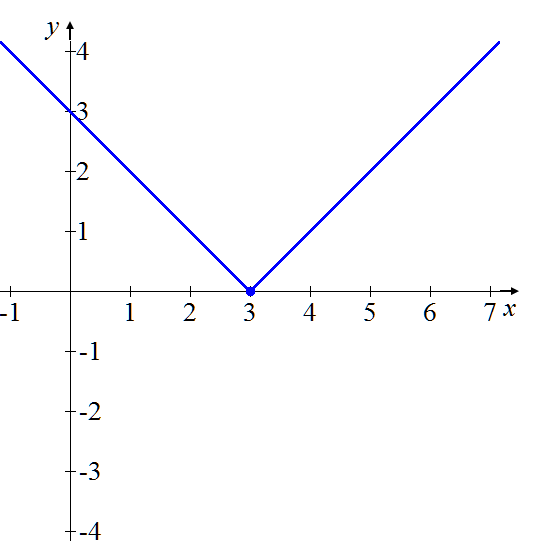
f (x) = | x – 3 |
Ejemplo ilustrativo 2.
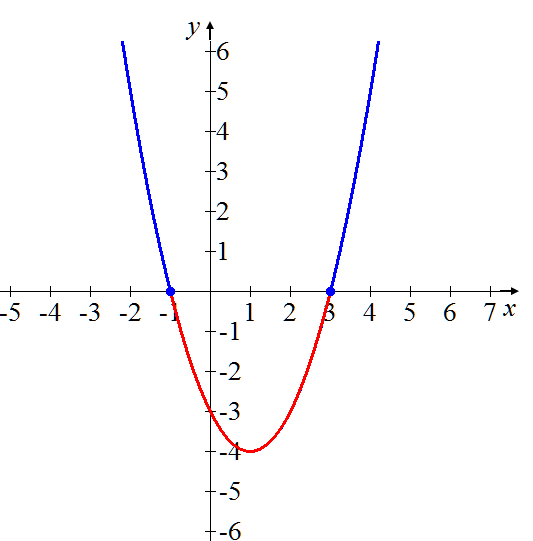
Si tenemos la función f (x) = x2 – 2 x – 3, su gráfica se muestra a continuación.

f (x) = x2 – 2 x – 3
Discriminemos la parte positiva de la función (azul), la cual se encuentra por encima del eje x y la negativa (roja), que se encuentra por debajo del eje x.
Para obtener la gráfica de la función valor absoluto correspondiente a la función f (x) = x2 – 2 x – 3, esto es, f (x) = | x2 – 2 x – 3 |, las partes positivas de la gráfica (azul) permanecen iguales y las negativas se reflejan sobre el eje x. El cero permanece igual en ambas. Se obtiene lo siguiente:
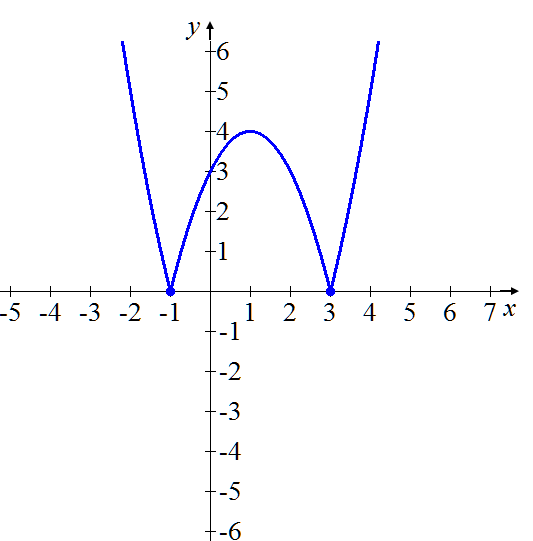
f (x) = | x2 – 2 x – 3 |
Si la función P (x) es positiva en todo su dominio, entonces la gráfica de f (x) = | P (x) | es igual a la gráfica de P (x), mientras que si la función P (x) es negativa en todo su dominio, entonces la gráfica de f (x) = | P (x) | será la reflexión de la curva sobre el eje horizontal.
Ejemplo ilustrativo 3.
Si tenemos la función f (x) = x2 + 2 x + 3, su gráfica se muestra a continuación.

Puesto que la función es positiva en todo su dominio (su gráfica se encuentra por encima del eje x), la gráfica de la función valor absoluto correspondiente es:

Valoraciones
No hay valoraciones aún.