Descripción
SOLUCIÓN DEL EJERCICIO.
f (x) = 2 x2 – 3 x + 4
Tipo de función.
Se trata de una función cuadrática f (x) = a x2 + b x + c.
Coeficientes de la función.
Al comparar la función dada f (x) = 2 x2 – 3 x + 4 con la forma general de la función cuadrática, f (x) = a x2 + b x + c, se tiene:
a = 2, b = – 3, c = 4.
Dominio de la función.
Dom f = ℝ
Forma de la gráfica de la función.
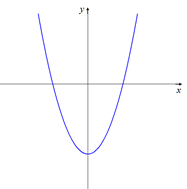
Puesto que a = 2 > 0, la parábola es cóncava hacia arriba.
Elementos de la gráfica de la función.
Coordenadas del vértice.
|
Coordenada x. \( \displaystyle x_V = \frac{-b}{2\,a}\) \( \displaystyle x_V = \frac{-(-3)}{2\,(2)}\) \( \displaystyle x_V = \frac{3}{4}\) |
Coordenada y. \( \displaystyle y_V = \frac{4\,a\,c-b^2}{4\,a}\) \( \displaystyle y_V = \frac{4\,(2)\,(4)-(-3)^2}{4\,(2)}\) \( \displaystyle y_V = \frac{32-9}{8}\) \( \displaystyle y_V = \frac{23}{8}\) |
Coordenadas del vértice.
\( \displaystyle V \left(\frac{3}{4},\frac{23}{8}\right)\)
En la figura siguiente se ilustra el punto V correspondiente al vértice de la parábola. Es importante mencionar que para graficar este punto en el papel, se debe usar aproximación a un decimal. En este caso, se ubica el punto (0.8 , 2.9) que son los valores aproximados a 3/4 y 23/8 respectivamente.

Puntos de intersección con los ejes.
Corte al eje y: ( 0 , c )
Corte al eje y: A ( 0 , 4)
En la figura siguiente se ilustra el punto A correspondiente al corte de la parábola con el eje y.

Corte al eje x.
Determinación del número de cortes con el eje x.
b2 – 4 a c = – 23 < 0. No existe corte con el eje x.
Hasta ahora se conocen sólo el vértice y el punto de corte con el eje y. Dos puntos adicionales de la gráfica se determinan asignándole valores a x (uno menor que la abcisa del vértice y otro mayor).
|
Para x = – 1: f (– 1) = 2 (– 1)2 – 3 (– 1) + 4 f (– 1) = 2 (1) + 3 + 4 f (– 1) = 9 |
Para x = 2: f (2) = 2 (2)2 – 3 (2) + 4 f (2) = 2 (4) – 6 + 4 f (2) = 6 |
El punto B ( – 1 , 9 ) pertenece a la gráfica de la función.
El punto C ( 2 , 6 ) pertenece a la gráfica de la función.
En la figura siguiente se ilustran los puntos B y C.

Gráfica de la función.
Con todos los puntos obtenidos se traza la parábola.

Rango de la función.
Siendo la parábola cóncava hacia arriba, y a partir de la figura anterior:
Rgo f = [ yV , + ∞ )
\( \text{Rgo}\,f = \left[\frac{23}{8},+\infty\right)\)
Valoraciones
No hay valoraciones aún.