Descripción
Función arco de circunferencia.
Definición de la función arco de circunferencia.
La función arco de circunferencia se define como \( f\,(x) = k\pm\sqrt{r^2-(x-h)^2}\)
h, k, r ϵ R h, k, r = Constantes.
El punto ( h , k ) representa el centro del arco de circunferencia. r es el radio del arco de circunferencia.
Es característica en la función arco de circunferencia la presencia de – x2 ó – (x – h)2 dentro de una raíz cuadrada.
Ejemplos de la función arco de circunferencia.
Son ejemplos de función arco de circunferencia:
\( f\,(x) = \sqrt{9-x^2}\)
\( f\,(x) = -\sqrt{25-x^2}\)
\( f\,(x) = \sqrt{9-(x-1)^2}\)
\( f\,(x) = 4-\sqrt{1-(x+2)^2}\)
No son ejemplos de función arco de circunferencia:
\( f\,(x) = \sqrt{9-x^{\color{Red}{\textbf{3}}}}\). Está permitida la forma 9 – x2, pero no 9 – x3. El grado de x dentro del radical debe ser 2.
\( f\,(x) = -\sqrt{25-x}\). Está permitida la forma 25 – x2, pero no 25 – x. El grado de x dentro del radical debe ser 2.
\( f\,(x) = \sqrt{9{\color{Red}{\textbf{+}}}(x-1)^2}\). Está permitida la forma 9 – (x – 1)2, pero no 9 + (x – 1)2. El coeficiente de x2 o de (x – h)2 debe ser – 1.
\( f\,(x) = \sqrt{9-{\color{Red}{\textbf{2}}}(x-1)^2}\). Está permitida la forma 9 – (x – 1)2, pero no 9 – 2 (x – 1)2. El coeficiente de x2 o de (x – h)2 debe ser – 1.
\( f\,(x) = 4-{\color{Red}{\textbf{3}}}\sqrt{1-(x+2)^2}\). El coeficiente del radical debe ser 1 ó – 1.
\( f\,(x) = 4-\sqrt{1-(x^{\color{Red}{\textbf{2}}}+2)^2}\). Está permitida la forma 1 – (x + 2)2, pero no 1 – (x2 + 2)2. El grado de x dentro del paréntesis debe ser 1.
\( f\,(x) = 4\,{\color{Red}{x}}-\sqrt{1-(x+2)^2}\). El término fuera del radical debe ser una constante.
Dominio de la función arco de circunferencia.
Dom f = [ h – r , h + r ]
Gráfica de la función arco de circunferencia.
|
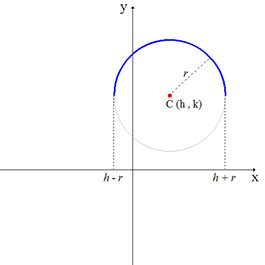
Arco superior. \( f\,(x) = k+\sqrt{r^2-(x-h)^2}\) |
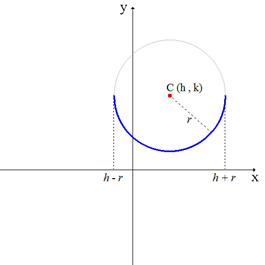
Arco inferior. \( f\,(x) = k-\sqrt{r^2-(x-h)^2}\) |
Arco superior: Coeficiente del radical igual a 1.
Arco inferior: Coeficiente del radical igual a – 1.
La gráfica de la función arco de circunferencia se puede obtener en forma práctica graficando el centro del arco, y con una longitud constante e igual al radio del mismo, trazar dicha gráfica. Se debe tener en cuenta si se trata del arco superior o del arco inferior de la circunferencia.
Rango de la función arco de circunferencia.
Depende del arco:
Arco superior: Rgo f = [ k , k + r ]
Arco inferior: Rgo f = [ k – r , k ]

Valoraciones
No hay valoraciones aún.