EJERCICIO 04

Descripción

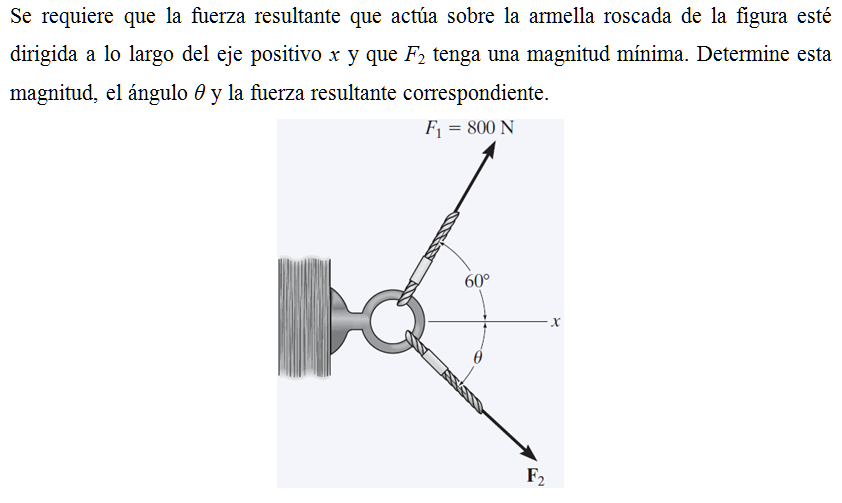
Se requiere que la fuerza resultante que actúa sobre la arnella roscada de la figura esté dirigida a lo largo del eje positivo x y que F₂ tenga una magnitud mínima. Determine esta magnitud, el ángulo α y la fuerza resultante correspondiente.

Referencia: Ejemplo 2.4 del Hibbeler, decimosegunda edición, página 26.

Solución.

F₁ = 800 N

Para que F₂ sea mínima, debe ser ortogonal a R. El diagrama vectorial se muestra a continuación.

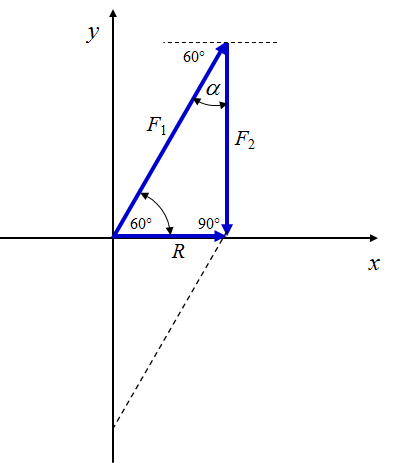
Cálculo de θ.

60° + θ = 90°

θ = 90° – 60°

θ = 30°

Cálculo de F₂.

Teorema del seno.

\( \displaystyle \frac{F_2}{\sin 60º}=\frac{F_1}{\sin 90º}\)

\( \displaystyle F_2=\frac{\sin 60º}{\sin 90º}F_1\)

\( \displaystyle F_2=\frac{\sin 60º}{\sin 90º}\times 800\)

F₂ = 692.82 N

Cálculo de la fuerza resultante R.

Teorema del seno.

\( \displaystyle \frac{R}{\sin\theta}=\frac{F_1}{\sin 90º}\)

\( \displaystyle R=\frac{\sin\theta}{\sin 90º}F_1\)

\( \displaystyle F_2=\frac{\sin 30º}{\sin 90º}\times 800\)

R = 400 N