EJERCICIO 01

Descripción

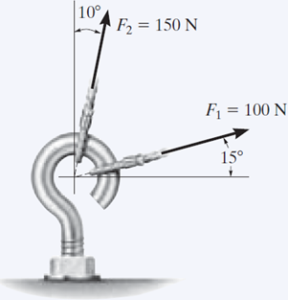
La armella roscada de la figura está sometida a dos fuerzas F₁ y F₂. Determine la magnitud y la dirección de la fuerza resultante.

Referencias:

Ejemplo 2-1 del Hibbeler. Décima Edición. Página 22.

Ejemplo 2-1 del Hibbeler. Decimosegunda Edición. Página 23.

Solución.

F₁ = 100 N

F₂ = 150 N

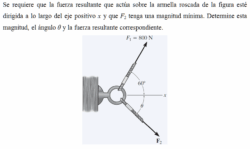
El diagrama vectorial se muestra a continuación. Se trasladó la fuerza F₁ de tal manera que su origen coincidiera con el extremo de F₂. De esta manera construimos un triángulo. La fuerza resultante F_R va desde el origen de F₂ hasta el extremo de F₁. Un triángulo equivalente al anterior se hubiese construido en el lado derecho si trasladamos la fuerza F₂  de tal manera que su origen coincidiera con el extremo de F₁.

Cálculo de α.

α = 10º + 90º + 15º

α = 115º

Módulo de la resultante.

Teorema del coseno.

\( \displaystyle F_R=\sqrt{F_1^2+F_2^2-2\,F_1F_2\cos\alpha}\)

\( \displaystyle F_R=\sqrt{(100)^2+(150)^2-2\,(100)\,(150)\cos115º}\)

\( \displaystyle F_R=\sqrt{10000+22500-(-12678.55)}\)

\( \displaystyle F_R=\sqrt{45178.55}\)

F_R = 212.55 N

Dirección de la resultante (con respecto al eje x).

Ángulo β entre la resultante y el vector F₂.

Teorema del seno.

\( \displaystyle \frac{F_R}{\sin\alpha}=\frac{F_1}{\sin\beta}\)

\( \displaystyle \sin\alpha=\frac{F_1}{F_R}\sin\alpha\)

\( \displaystyle \sin\alpha=\frac{100}{212.55}\sin 115º\)

sen β = 0.4264

β = sen^–1 (0.4264)

β = 25.24°

Dirección de la resultante:

θ = 10° + 25.24°

θ = 35.24° a la derecha del semieje positivo de las y.

θ = 54.76° por encima del semieje positivo de las x ( ).