Descripción
Ecuaciones de una recta en R3.
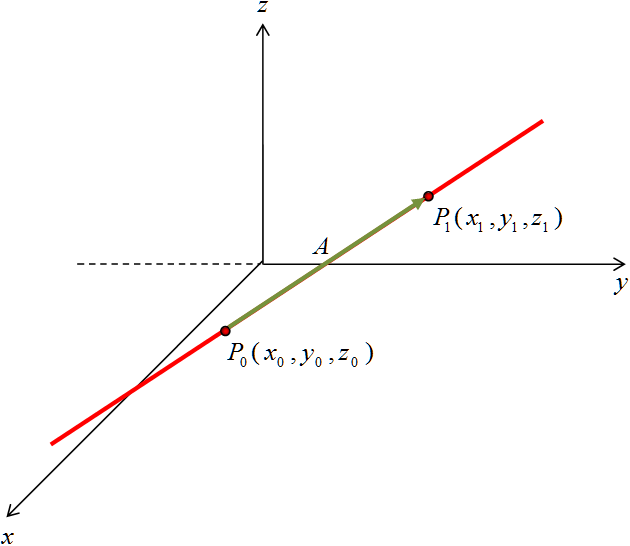
Una recta L que pasa por el punto P ( x0 , y0 , z0 ) y cuyo vector director es A = a i + b j + c k puede describirse mediante:
a) Ecuaciones paramétricas:
| x = x0 + a t | y = y0 + b t | z = z0 + c t |
Es importante mencionar que el parámetro t es una variable que a medida que va tomando valores, las ecuaciones paramétricas van definiendo las coordenadas x, y y z de puntos que pertenecen a la recta.
b) Ecuación simétrica:
\( \displaystyle \frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}\)
Si uno o dos de los números directores (a, b ó c) de L son cero, no podemos usar la forma simétrica tal como está escrita. En tales casos, debemos emplear las relaciones paramétricas. Por ejemplo, digamos que a = 0, pero b y c son ambas diferentes de cero. Entonces por las ecuaciones paramétricas, tenemos para las ecuaciones de L:
x = x0 + (0) t
y = y0 + b t
y
z = z0 + c t ó
| x = x0 | y = y0 + b t | z = z0 + c t |
las cuales, de acuerdo con la forma simétrica, pueden escribirse como
x = xo, \( \displaystyle \frac{y-y_0}{b}=\frac{z-z_0}{c}\)
c) Ecuación vectorial paramétrica:
P = P0 + A t, o su forma equivalente:
P ( x , y , z ) = (x0 , y0, z0) + < a , b , c > t
Si se conocen dos puntos de la recta, P0(x0 , y0, z0) y P1(x1 , y1, z1), entonces el vector director es:
A = P0P1
A = (x1 – x0) i + (y1 – y0) j + (z1 – z0) k
Para definir las ecuaciones de una recta en el espacio, así como se utiliza el vector P0P1 como vector director de la recta, también se puede utilizar el vector P1P0 (su opuesto) ó cualquier vector paralelo a éstos, por lo cual puede afirmarse que la ecuación de una recta en R3 no es única.
Una recta puede ser expresada mediante cualquiera de las tres formas mencionadas anteriormente, e incluso dichas formas pueden ser convertidas una en otras.
Si se conocen las ecuaciones paramétricas:
| x = x0 + a t | y = y0 + b t | z = z0 + c t |
La forma simétrica correspondiente se obtiene al despejar t de cada una de las ecuaciones y escribir una igualdad:
\( \displaystyle t=\frac{x-x_0}{a}\)
\( \displaystyle t=\frac{y-y_0}{b}\)
\( \displaystyle t=\frac{z-z_0}{c}\), obteníendose:
\( \displaystyle \frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}\)
La forma vectorial paramétrica se obtiene mediante el punto, que corresponde a los términos independientes en x, y y z y el vector director, cuyas componentes corresponden a los coeficientes del parámetro t en las ecuaciones paramétricas.
P ( x , y , z ) = (x0 , y0, z0) + < a , b , c > t
Si se conoce la ecuación simétrica:
\( \displaystyle \frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}\)
La forma paramétrica correspondiente se obtiene al igualar todos los miembros de la ecuación al parámetro t y despejar las variables x, y y z:
\( \displaystyle \frac{x-x_0}{a}=t\)
\( \displaystyle \frac{y-y_0}{b}=t\)
\( \displaystyle \frac{z-z_0}{c}=t\), obteniéndose:
| x = x0 + a t | y = y0 + b t | z = z0 + c t |
La forma vectorial paramétrica se obtiene mediante el punto, que corresponde a los valores de x, y y z que anulan el numerador en cada término y el vector director, cuyas componentes corresponden a los denominadores de la ecuación.
P ( x , y , z ) = (x0 , y0, z0) + < a , b , c > t
Si se conoce la ecuación vectorial paramétrica, la escritura de las ecuaciones paramétricas o simétricas es inmediata.

Valoraciones
No hay valoraciones aún.