Descripción
SOLUCIÓN DEL EJERCICIO.
f (x) = x2 + 4 x + 3
Tipo de función.
Se trata de una función cuadrática f (x) = a x2 + b x + c.
Coeficientes de la función.
Al comparar la función dada f (x) = x2 + 4 x + 3 con la forma general de la función cuadrática, f (x) = a x2 + b x + c, se tiene:
a = 1, b = 4, c = 3.
Dominio de la función.
Dom f = ℝ
Forma de la gráfica de la función.
Puesto que a = 1 > 0, la parábola es cóncava hacia arriba.
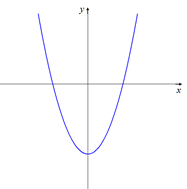
Elementos de la gráfica de la función.
Coordenadas del vértice.
|
Coordenada x. \( \displaystyle x_V = \frac{-b}{2\,a}\) \( \displaystyle x_V = \frac{-4}{2\,(1)}\) \( \displaystyle x_V = \frac{-4}{2}\) xV = – 2 |
Coordenada y. \( \displaystyle y_V = \frac{4\,a\,c-b^2}{4\,a}\) \( \displaystyle y_V = \frac{4\,(1)\,(3)-(4)^2}{4\,(1)}\) \( \displaystyle y_V = \frac{12-16}{4}\) \( \displaystyle y_V = \frac{-4}{4}\) yV = – 1 |
Coordenadas del vértice.
V ( – 2 , – 1 )
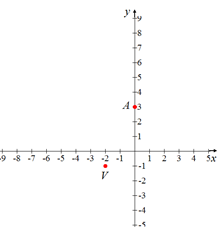
En la figura siguiente se ilustra el punto V correspondiente al vértice de la parábola.

Puntos de intersección con los ejes.
Corte al eje y: ( 0 , c )
Corte al eje y: A ( 0 , 3)
En la figura siguiente se ilustra el punto A correspondiente al corte de la parábola con el eje y.
Corte al eje x.
Determinación del número de cortes con el eje x.
b2 – 4 a c = 4 > 0. Existen dos cortes con el eje x.
Los valores de la abcisa en el punto de corte con el eje x se determina con la ecuación:
\( \displaystyle x = \frac{-b\pm\sqrt{b^2-4\,a\,c}}{2\,a}\)
La ordenada correspondiente de dichos puntos es 0.
Al sustituir valores:
\( \displaystyle x = \frac{-(4)\pm\sqrt{4}}{2\,(1)}\)
\( \displaystyle x = \frac{-4\pm2}{2}\)
Se obtienen dos valores para x.
|
\( \displaystyle x_1 = \frac{-4-2}{2}\) \( \displaystyle x_1 = \frac{-6}{2}\) x1 = – 3 |
\( \displaystyle x_2 = \frac{-4+2}{2}\) \( \displaystyle x_2 = \frac{-2}{2}\) x2 = – 1 |
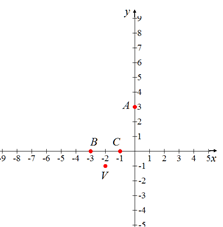
Cortes al eje x: B ( – 3 , 0 ) y C ( – 1 , 0 ).
En la figura siguiente se ilustran los puntos B y C correspondientes a los cortes de la parábola con el eje x.
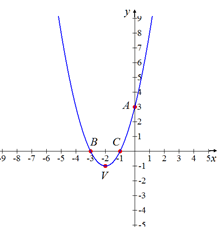
Gráfica de la función.
Con todos los puntos obtenidos se traza la parábola.
Rango de la función.
Siendo la parábola cóncava hacia arriba, y a partir de la figura anterior:
Rgo f = [ yV , + ∞ )
Rgo f = [ – 1 , + ∞ )
Valoraciones
No hay valoraciones aún.