EJERCICIO 31

Descripción

Un cilindro de 200 kg se sostiene por medio de dos cables AB y AC que se amarran en la parte más alta de una pared vertical. Una fuerza horizontal P perpendicular a la pared lo sostiene en la posición mostrada. Determine la magnitud de P y la tensión en cada cable.

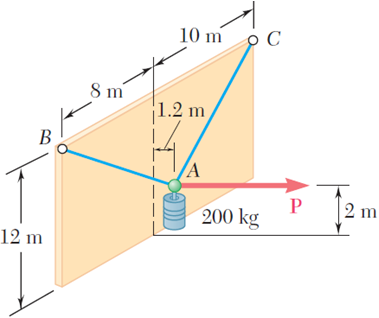
A 200-kg cylinder is hung by means of two cables AB and AC, which are attached to the top of a vertical wall. A horizontal force P perpendicular to the wall holds the cylinder in the position shown. Determine the magnitude of P and the tension in each cable.

Referencias:

Problema Resuelto 2.9 del Beer – Johnston. Novena Edición. Página 58.

Sample Problem 2.9 from Beer – Johnston. Ninth Edition. Page 58.

Problema Resuelto 2.9 del Beer – Johnston. Décima Edición. Página 48.

Sample Problem 2.9 from Beer – Johnston. Tenth Edition. Page 59.

Solución.

Diagrama de cuerpo libre.

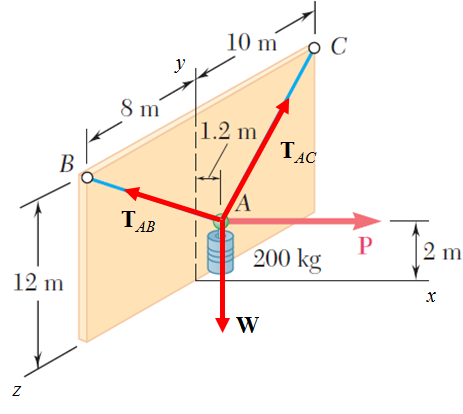
Condición de equilibrio: Σ F = 0

P + W + T_AB + T_AC = 0

Fuerzas individuales.

P = || P || i

W = – || W || j

W = (– 200 × 9.81 j) N

W = (– 1962 j) N

Fuerza en el cable AB.

T_AB = || T_AB || u_AB

u_AB: vector unitario en la dirección de la fuerza.

Coordenadas del punto A: A ( 1.2 , 2 , 0 )

Coordenadas del punto B: B ( 0 , 12 , 8 )

Vector AB.

AB = (0 – 1.2) i + (12 – 2) j + (8 – 0) k

AB = – 1.2 i + 10 j + 8 k

Módulo del vector AB:

\( \displaystyle \vert\vert\;AB\,\vert\vert=\sqrt{(-1.2)^2+(10)^2+(8)^2}\)

\( \displaystyle \vert\vert\;AB\,\vert\vert=\sqrt{1.44+100+64}\)

\( \displaystyle \vert\vert\;AB\,\vert\vert=\sqrt{165.44}\)

|| AB || = 12.8623

\( \displaystyle \mathbf{u}_{AB}=\frac{-1.2\,\mathbf{i}+10\,\mathbf{j}+8\,\mathbf{k}}{12.8623}\)

u_AB = – 0.0933 i + 0.7775 j + 0.6220 k

T_AB = || T_AB || (– 0.0933 i + 0.7775 j + 0.6220 k)

T_AB = – 0.0933 || T_AB || i + 0.7775 || T_AB || j + 0.6220 || T_AB || k

Fuerza en el cable AC.

T_AC = || T_AC || u_AC

u_AC: vector unitario en la dirección de la fuerza.

Coordenadas del punto A: A ( 1.2 , 2 , 0 )

Coordenadas del punto C: C ( 0 , 12 , –10 )

Vector AC.

AC = (0 – 1.2) i + (12 – 2) j + (–10 – 0) k

AC = – 1.2 i + 10 j – 10 k

Módulo del vector AC:

|| AC || = 14.1930

u_AC = – 0.0845 i + 0.7046 j – 0.7046 k

T_AC = || T_AC || (– 0.0845 i + 0.7046 j – 0.7046 k)

T_AC = – 0.0845 || T_AC || i + 0.7046 || T_AC || j – 0.7046 || T_AC || k

Componentes rectangulares de las fuerzas individuales:

Vector	Componente x	Componente y	Componente z
P	|| P ||	0	0
TAB	– 0.0933 || TAB ||	0.7775 || TAB ||	0.6220 || TAB ||
TAC	– 0.0845 || TAC ||	0.7046 || TAC ||	– 0.7046 || TAC ||
W	0	– 1962	0

Al aplicar la condición de equilibrio (Σ F_x = 0, Σ F_y = 0 y Σ F_z = 0), se obtiene el siguiente sistema de ecuaciones:

|| P || – 0.0933 || T_AB || – 0.0845 || T_AC || = 0 (1)

0.7775 || T_AB || + 0.7046 || T_AC || = 1962 (2)

0.6220 || T_AB || – 0.7046 || T_AC || = 0 (3)

De la ecuación (3):

0.6220 || T_AB || = 0.7046 || T_AC ||

\( \displaystyle \vert\vert\;T_{AB}\,\vert\vert=\frac{0.7046}{0.6220}\vert\vert\;T_{AC}\,\vert\vert\)

|| T_AB || = 1.1328 || T_AC || (4)

Al sustituir la ecuación (4) en la ecuación (2):

0.7775 (1.1328 || T_AC ||) + 0.7046 || T_AC || = 1962

0.8808 || T_AC || + 0.7046 || T_AC || = 1962

1.5854 || T_AC || = 1962

\( \displaystyle \vert\vert\;T_{AC}\,\vert\vert=\frac{1962}{1.5854}\)

|| T_AC || = 1237.54 N

De la ecuación (4):

|| T_AB || = 1.1328 (1237.54 N)

|| T_AB || = 1401.89 N

De la ecuación (1):

|| P || – 0.0933 || T_AB || – 0.0845 || T_AC || = 0

|| P || – 0.0933 (1401.89 N) – 0.0845 (1237.54 N) = 0

|| P || – 130.80 N – 104.57 N = 0

|| P || – 235.37 N = 0

|| P || = 235.37 N

La magnitud de P y la tensión en cada cable es:

|| P || = 235.37 N

|| T_AB || = 1401.89 N

|| T_AC || = 1237.54 N