Descripción
Calcular \(\displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x\)
Referencias:
Ejemplo 5. Sección 9.4 del Thomas. Sexta Edición. Página 427.
Ejemplo 118 del Filippis. Página 292.
Ejemplo 6.6 del Cortés. Octava Edición. Página 169.
Exercise 7. Section 108 from James Michie. Page 193.
Ejemplo 1. Sección 7.5 del Zill – Wright. Cuarta Edición. Página 400.
Solución.
El integrando tiene la forma \( \displaystyle\sqrt{a^2-u^2}\), se hace la sustitución:
| x = 3 sen θ | d x = 3 cos θ d θ | \( \sqrt{9 – x^2} = \sqrt{9 – (3 \sin \theta)^2} \) |
| \(\sqrt{9 – x^2}= \sqrt{9 – 9 \sin^2 \theta} \) | ||
| \(\sqrt{9 – x^2}= \sqrt{9\,(1 – \sin^2 \theta)} \) | ||
| \(\sqrt{9 – x^2}= \sqrt{9 \cos^2 \theta} \) | ||
| \(\sqrt{9 – x^2}= 3 \cos \theta \) |
Al sustituir x = 3 sen θ, d x = 3 cos θ d θ y en la integral:
\( \displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x=\int\frac{(3\,\sin\theta)^2(3\cos\theta\,d\,theta)}{3\,\cos\theta}\)
Al simplificar los valores numéricos y el factor cos θ:
\( \displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x=\int(3 \sin\theta)^2d\,\theta\)
\( \displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x=\int 9\,\sin^2\theta\,d\,\theta\)
\( \displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x=9\int \sin^2\theta\,d\,\theta\)
La integral anterior se resuelve aplicando integración de potencias de funciones trigonométricas.
\( \displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x=9\int (\frac{1}{2}-\frac{1}{2}\cos2\,\theta)\,d\,\theta\)
\( \displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x=\frac{9}{2}\int d\,\theta-\frac{9}{2}\int\cos2\,\theta\,d\,\theta\)
La integración conduce a:
\( \displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x=\frac{9}{2}\theta-\frac{9}{2}(\frac{1}{2}\sin2\,\theta)+C\)
\( \displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x=\frac{9}{2}\theta-\frac{9}{4}\sin2\,\theta+C\)
Para volver a la variable inicial, no es posible definir en forma directa sen 2 θ en función de x, por lo cual se aplica la identidad sen 2 θ = 2 sen θ cos θ
\( \displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x=\frac{9}{2}\theta-\frac{9}{4}(2\,\sin\theta\,\cos\theta)+C\)
\( \displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x=\frac{9}{2}\theta-\frac{9}{2}\sin\theta\,\cos\theta+C\) (1)
Para volver a la variable original se debe definir θ, sen θ y cos θ en función de x.
Partiendo de la sustitución trigonométrica realizada:
x = 3 sen θ
\( \displaystyle \sin\theta=\frac{x}{3}=\frac{\text{Cateto opuesto}}{\text{Hipotenusa}}\)
Se construye un triángulo rectángulo cuyo cateto opuesto es x e hipotenusa es 3. El lado faltante, se determina con la aplicación del teorema de Pitágoras.
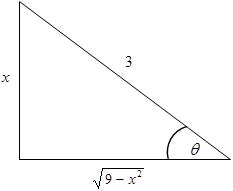
Observe que la magnitud del lado faltante coincide con la expresión \( \displaystyle\sqrt{9-x^2}\) que se encuentra en el integrando.
A partir del triángulo obtenido, se define θ, sen θ y cos θ.
\( \displaystyle \theta=\sin^{-1}\left(\frac{x}{3}\right)\) (2)
\( \displaystyle \sin\theta=\frac{\text{Cateto opuesto}}{\text{Hipotenusa}}\)
\( \displaystyle \sin\theta=\frac{x}{3}\) (3)
\( \displaystyle \cos\theta=\frac{\text{Cateto adyacente}}{\text{Hipotenusa}}\)
\( \displaystyle \cos\theta=\frac{\sqrt{9-x^2}}{3}\) (4)
Al sustituir las ecuaciones (2), (3) y (4) en la ecuación (1):
\( \displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x=\frac{9}{2}\left[\sin^{-1}\left(\frac{x}{3}\right)\right]-\frac{9}{2}\left(\frac{x}{3}\right)\,\left(\frac{\sqrt{9-x^2}}{3}\right)+C\)
\( \displaystyle\int\frac{x^2}{\sqrt{9-x^2}}d\,x=\frac{9}{2}\sin^{-1}\left(\frac{x}{3}\right)-\frac{1}{2}x\sqrt{9-x^2}+C\)



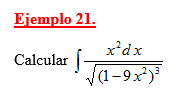
Valoraciones
No hay valoraciones aún.