EJERCICIO 19

Descripción

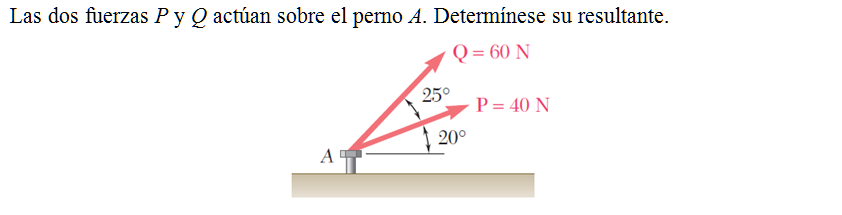
Las dos fuerzas P y Q actúan sobre el perno A. Determínese su resultante.

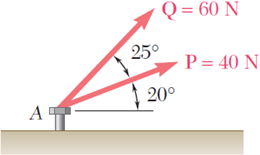
The two forces P and Q act on a bolt A. Determine their resultant.

Referencias:

Problema Resuelto 2.1 del Beer – Johnston. Séptima Edición. Página 22.

Problema Resuelto 2.1 del Beer – Johnston. Octava Edición. Página 22.

Problema Resuelto 2.1 del Beer – Johnston. Novena Edición. Página 22.

Sample Problem 2.1 from Beer – Johnston. Ninth Edition. Page 22.

Problema Resuelto 2.1 del Beer – Johnston. Décima Edición. Página 18.

Sample Problem 2.1 from Beer – Johnston. Tenth Edition. Page 22.

Solución.

P = 40 N

Q = 60 N

El diagrama vectorial se muestra a continuación. Se trasladó la fuerza Q de tal manera que su origen coincidiera con el extremo de P. De esta manera construimos un triángulo. La fuerza resultante R va desde el origen de P hasta el extremo de Q. Un triángulo equivalente al anterior se hubiese construido en el lado izquierdo si trasladamos la fuerza P  de tal manera que su origen coincidiera con el extremo de Q.

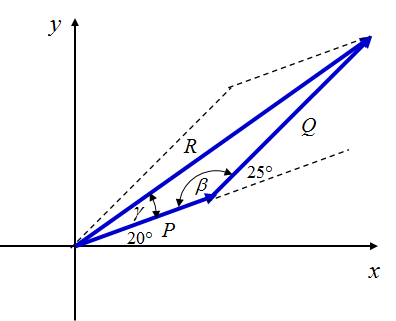
Cálculo de β.

β + 25º = 180°

β = 180° – 25°

β = 155°

Módulo de la resultante.

Teorema del coseno.

\( \displaystyle R=\sqrt{P^2+Q^2-2\,P\,Q\cos\beta}\)

\( \displaystyle R=\sqrt{(40)^2+(60)^2-2\,(40)\,(60)\cos 155º}\)

\( \displaystyle R=\sqrt{1600+3600-(-4350.28)}\)

\( \displaystyle R=\sqrt{9550.28}\)

R = 97.73 N

Dirección de la resultante (con respecto al eje x).

Ángulo γ entre la resultante y el vector P.

Teorema del seno.

\( \displaystyle \frac{R}{\sin\beta}=\frac{Q}{\sin\gamma}\)

\( \displaystyle \sin\gamma=\frac{Q}{R}\sin\beta\)

\( \displaystyle \sin\gamma=\frac{60}{97.73}\sin 155º\)

sen γ = 0.2595

γ = sen^–1 (0.2595)

γ = 15.04°

Dirección de la resultante:

α = 20º + γ

α = 20° + 15.04°

α = 35.04° por encima del semieje positivo de las x ( ).