Descripción
Flujo de una película descendente. Consideremos una superficie plana inclinada. Estas películas se han estudiado en relación con torres de pared mojada, experiencias de evaporación y absorción de gases y aplicación de capas de pintura a rollos de papel. Se supone que la viscosidad y densidad del fluido son constantes y se considera una región de longitud L, suficientemente alejada de los extremos de la pared, de forma que las perturbaciones de la entrada y la salida no están incluidas en L; es decir, que en esta región el componente vz de velocidad es independiente de z.
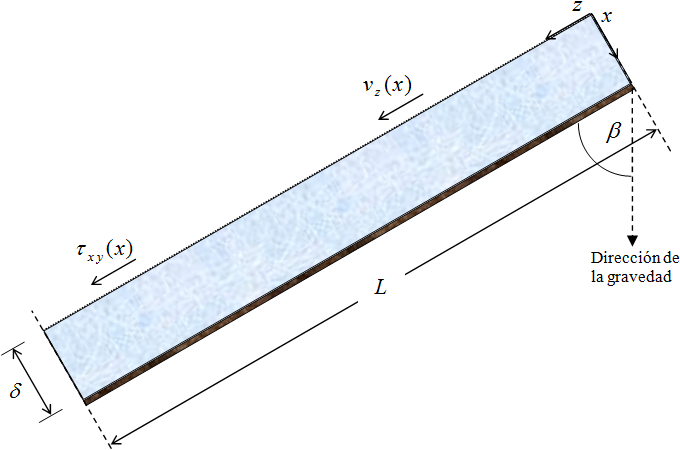
Determinar:
a) Distribución de la densidad de flujo de cantidad de movimiento.
b) Distribución de velocidad.
c) Velocidad máxima.
d) Velocidad media.
e) Velocidad volumétrica de flujo (Caudal).
f) Espesor de la película.
g) Componente de la fuerza F del fluido sobre la superficie.
Referencia: Sección 2.2 del Bird. Página 2-4.
SOLUCIÓN DEL EJERCICIO.
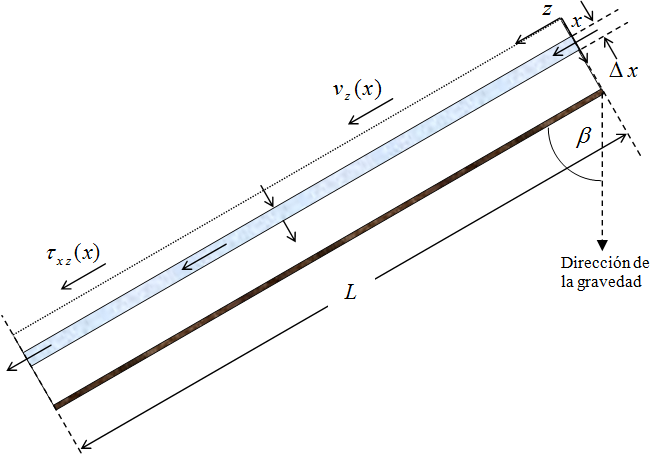
a) Vista de frente:
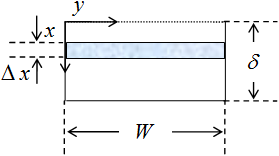
Condiciones:
Estado estacionario.
Flujo laminar.
Fluido Newtoniano.
Propiedades del fluido constantes (ρ, μ).
Efectos de borde despreciables.
Flujo en dirección z (vx = 0, vy = 0, vz ≠ 0).
La velocidad varía en función de x: vz = vz (x).
Balance de cantidad de movimiento.
L W τxz | x – L W τxz | x + ∆ x + L W ∆ x ρ gz + (p0 – pL) W ∆ x = 0
Flujo sin diferencia de presión (p0 – pL = 0).
L W τxz | x – L W τxz | x + ∆ x + L W ∆ x ρ gz = 0
gz es la componente gravitacional en la dirección del flujo. En este caso gz = g cos β.
L W τxz | x – L W τxz | x + ∆ x + L W ∆ x ρ g cos β = 0 (1)
Al simplificar L W:
τxz | x – τxz | x + ∆ x + ∆ x ρ g cos β = 0
τxz | x – τxz | x + ∆ x = – ∆ x ρ g cos β
τxz | x + ∆ x – τxz | x = ∆ x ρ g cos β
\( \displaystyle \frac{\tau_{xz} \big|_{x + \Delta\,x} – \tau_{xz} \big|_{x}}{\Delta\,x} = \rho\, g\cos\beta\)
Tomando el límite cuando ∆ x → 0 en la ecuación anterior:
\( \displaystyle \lim_{\Delta\,x \to 0}\frac{\tau_{xz} \big|_{x + \Delta\,x} – \tau_{xz} \big|_{x}}{\Delta\,x} = \lim_{\Delta\,x \to 0}\rho\, g\cos\beta\)
\( \displaystyle \lim_{\Delta\,x \to 0}\frac{\tau_{xz} \big|_{x + \Delta\,x} – \tau_{xz} \big|_{x}}{\Delta\,x} = \rho\, g\cos\beta\)
Aplicando la definición de derivada:
\( \displaystyle \frac{d\,\tau_{xz}}{d\,x} = \rho\, g\cos\beta\)
Al separar variables en la ecuación anterior:
d τxz = ρ g cos β d x
Integrando ambos miembros de la ecuación:
\( \displaystyle \int d\,\tau_{xz} = \int \rho\, g\cos\beta\,d\,x\)
\( \displaystyle \tau_{xz} = \rho\, g\cos\beta\int d\,x\)
La integración conduce a:
τxz = ρ g cos β x + C1 (2)
Condición de borde: Para x = 0, τxz = 0.
Al sustituir en la ecuación (2):
0 = ρ g cos β (0) + C1
C1 = 0 (3)
Al sustituir la ecuación (3) en la ecuación (2):
τxz = ρ g cos β x (4)
La ecuación (4) es la distribución de la densidad de flujo de cantidad de movimiento.
b) Distribución de velocidad.
Fluido Newtoniano.
\( \displaystyle \tau_{xz} = -\mu \frac{d\,v_z}{d\,x}\) (5)
Al sustituir la ecuación (5) en la ecuación (4):
\( \displaystyle -\mu \frac{d\,v_z}{d\,x}=\rho\, g\cos\beta\,x\)
Al separar las variables en la ecuación anterior:
\( \displaystyle d\,v_z=-\frac{\rho\, g\cos\beta}{\mu} x\,d\,x\)
Al integrar ambos miembros de la ecuación:
\( \displaystyle \int d\,v_z=-\int\frac{\rho\, g\cos\beta}{\mu} x\,d\,x\)
\( \displaystyle v_z=-\frac{\rho\, g\cos\beta}{\mu}\int x\,d\,x\)
La integración conduce a:
\( \displaystyle v_z=-\frac{\rho\, g\cos\beta}{\mu}\left(\frac{x^2}{2}\right)+C_2 \)
\( \displaystyle v_z=-\frac{\rho\, g\cos\beta}{2\,\mu}x^2+C_2 \) (6)
Condición de borde: Para x = δ, vz = 0.
Al sustituir en la ecuación (6):
\( \displaystyle 0=-\frac{\rho\, g\cos\beta}{2\,\mu}(\delta)^2+C_2 \)
Al despejar C2 en la ecuación anterior:
\( \displaystyle C_2=\frac{\rho\, g\cos\beta}{2\,\mu}\delta^2 \) (7)
Al sustituir la ecuación (7) en la ecuación (6):
\( \displaystyle v_z=-\frac{\rho\, g\cos\beta}{2\,\mu}x^2+\frac{\rho\, g\cos\beta}{2\,\mu}\delta^2 \)
\( \displaystyle v_z=\frac{\rho\, g\cos\beta}{2\,\mu}(\delta^2-x^2) \)
Al multiplicar y dividir por δ2:
\( \displaystyle v_z=\frac{\rho\, g\cos\beta}{2\,\mu}(\delta^2-x^2)\times\frac{\delta^2}{\delta^2} \)
\( \displaystyle v_z=\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\left(\frac{\delta^2-x^2}{\delta^2} \right)\)
\( \displaystyle v_z=\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\left(\frac{\delta^2}{\delta^2}-\frac{x^2}{\delta^2} \right)\)
\( \displaystyle v_z=\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\left(1-\frac{x^2}{\delta^2} \right)\)
\( \displaystyle v_z=\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\left[1-\left(\frac{x}{\delta}\right)^2 \right]\) (8)
Distribución de velocidad parabólico.
c) Velocidad máxima.
La velocidad es máxima en x = 0.
vz,max = vz (0)
Al sustituir x = 0 en la ecuación (8):
\( \displaystyle v_z=-\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\left[1-\left(\frac{0}{\delta}\right)^2 \right]\)
\( \displaystyle v_z=-\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\) (9)
d) Velocidad media.
Por definición:
\( \displaystyle <v_z=\frac{\text{Caudal}}{\text{Area de flujo}}\)
\( \displaystyle <v_z> = \displaystyle \frac{\int_0^W\int_0^{\delta}v_z\,d\,x\,d\,y}{\int_0^W\int_0^{\delta}d\,x\,d\,y}\) (10)
Al sustituir la ecuación (8) en la ecuación (10):
\( \displaystyle <v_z> = \frac{\int_0^W\int_0^{\delta}\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\left[1-\left(\frac{x}{\delta}\right)^2 \right]\,d\,x\,d\,y}{\int_0^W\int_0^{\delta}d\,x\,d\,y}\)
\( \displaystyle <v_z> = \frac{\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\int_0^W\int_0^{\delta}\left[1-\left(\frac{x}{\delta}\right)^2 \right]\,d\,x\,d\,y}{\int_0^W\int_0^{\delta}d\,x\,d\,y}\)
\( \displaystyle <v_z> = \frac{\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\int_0^W\int_0^{\delta}\left(1-\frac{x^2}{\delta^2}\right)\,d\,x\,d\,y}{\int_0^W\int_0^{\delta}d\,x\,d\,y}\)
Integrando con respecto a x.
\( \displaystyle <v_z> = \frac{\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\int_0^W\left(x-\frac{1}{3\,\delta^2}x^3\bigg\vert_0^{\delta}\right)d\,y}{\int_0^W \left(x\,\bigg\vert_0^{\delta}\right)\,d\,y}\)
\( \displaystyle <v_z> = \frac{\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\int_0^W\left(\delta-\frac{\delta}{3}\right)d\,y}{\int_0^W \delta\,d\,y}\)
\( \displaystyle <v_z> = \frac{\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\int_0^W\frac{2}{3}\delta\,d\,y}{\int_0^W \delta\,d\,y}\)
\( \displaystyle <v_z> = \frac{\frac{\rho\,g\,\delta^2\cos\beta}{2\,\mu}\times\frac{2}{3}\int_0^W\delta\,d\,y}{\int_0^W \delta\,d\,y}\)
\( \displaystyle <v_z> = \frac{\frac{\rho\,g\,\delta^3\cos\beta}{3\,\mu}\int_0^W d\,y}{\delta\int_0^W d\,y}\)
\( \displaystyle <v_z> = \frac{\frac{\rho\,g\,\delta^3\cos\beta}{3\,\mu}\left(y\,\bigg\vert_0^W\right)}{\delta \left(y\,\bigg\vert_0^W\right)}\)
\( \displaystyle <v_z> = \frac{\frac{\rho\,g\,\delta^3\cos\beta}{3\,\mu}(W-0)}{\delta\,(W-0)}\)
\( \displaystyle <v_z> = \frac{\frac{\rho\,g\,\delta^3\cos\beta}{3\,\mu}W}{\delta\,W}\)
\( \displaystyle <v_z> = \frac{\frac{\rho\,g\,W\,\delta^3\cos\beta}{3\,\mu}}{\delta\,W}\)
\( \displaystyle <v_z> = \frac{\rho\,g\,\delta^2\cos\beta}{3\,\mu}\) (11)
Comentario del autor:
En la deducción anterior, se omitió la simplificación de factores con el objeto de ilustrar que el caudal \( \displaystyle Q = \frac{\rho\,g\,W\,\delta^3\cos\beta}{3\,\mu}\) es mientras que el área de flujo es A = δ W. En la práctica, se tiene el mismo procedimiento y resultado de calcular el caudal y el área de flujo de manera independiente.
e) Velocidad volumétrica de flujo (Caudal).
Q = < vz > A (12)
Área perpendicular al flujo:
A = W δ (13)
Al sustituir las ecuaciones (11) y (13) en la ecuación (12):
\( \displaystyle Q = \left(\frac{\rho\,g\,W\,\delta^3\cos\beta}{3\,\mu}\right)(\delta\,W)\)
\( \displaystyle Q = \frac{\rho\,g\,W\,\delta^3\cos\beta}{3\,\mu}\) (14)
Flujo másico por unidad de ancho de la lámina ( \( \displaystyle \Gamma = \frac{m}{W}\)).
\( \displaystyle \rho = \frac{m}{Q}\) → \( \displaystyle Q = \frac{m}{\rho}\) (15)
Al sustituir la ecuación (15) en la ecuación (14):
\( \displaystyle \frac{m}{\rho} = \frac{\rho\,g\,W\,\delta^3\cos\beta}{3\,\mu}\)
\( \displaystyle \frac{m}{W} = \frac{\rho^2\,g\,W\,\delta^3\cos\beta}{3\,\mu}\)
\( \displaystyle \Gamma = \frac{\rho^2\,g\,W\,\delta^3\cos\beta}{3\,\mu}\) (16)
f) Espesor de la película.
Al despejar δ en la ecuación (11):
\( \displaystyle \delta^2 = \frac{3\,\mu\,<v_z>}{\rho\,g\,\cos\beta}\)
\( \displaystyle \delta = \sqrt{\frac{3\,\mu\,<v_z>}{\rho\,g\,\cos\beta}}\) (17)
Al despejar δ en la ecuación (14):
\( \displaystyle \delta^3 = \frac{3\,\mu\,Q}{\rho\,g\,W\,\cos\beta}\)
\( \displaystyle \delta = \sqrt[3]{\frac{3\,\mu\,Q}{\rho\,g\,W\,\cos\beta}}\) (18)
Al despejar δ en la ecuación (16):
\( \displaystyle \delta^3 = \frac{3\,\mu\,\Gamma}{\rho^2\,g\,W\,\cos\beta}\)
\( \displaystyle \delta = \sqrt[3]{\frac{3\,\mu\,\Gamma}{\rho^2\,g\,W\,\cos\beta}}\) (19)
g) Componente de la fuerza F del fluido sobre la superficie.
Fz (x) = τxz A (20)
De la ecuación (4):
τxz = ρ g cos β x (4)
Área de contacto.
A = L W (21)
Al sustituir las ecuaciones (4) y (21) en la ecuación (20):
Fz (x) = (ρ g cos β x) (L W)
Fz (x) = ρ g L W cos β x (22)
Para la capa de fluido sobre la superficie x = δ. Al evaluar la ecuación (22) en x = δ:
Fz (δ) = ρ g L W cos β (δ)
Fz (δ) = ρ g δ L W cos β (23)





Valoraciones
No hay valoraciones aún.