Descripción

Cáscaras semiesféricas.

\( \displaystyle q = \int_{r_0}^{r_1}\sigma\,(r)\,d\,A \)

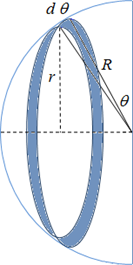
El elemento diferencial de área es la longitud del elemento (2 π r) multiplicada por el espesor del mismo (R d θ).

d A = 2 π r × R d θ

\( \displaystyle \cos\theta=\frac{r}{R} \)

r = R cos θ, \( \displaystyle 0\leq\theta\leq \pi/2 \)

d A = 2 π (R cos θ) × R d θ

d A = 2 π R² cos θ d θ

\( \displaystyle q = \int_{\theta_0}^{\theta_1}\sigma\,(\theta)\,(2\,\pi\,R^2\cos\theta\,d\,\theta) \)