Descripción
Hallar la siguiente integral, emplendo sustitución trigonométrica \( \displaystyle \int \frac{x^2d\,x}{\sqrt{1-x^2}}\).
Referencia: Problema 1201 del Demidovich. Página 181.
Respuesta: \( \displaystyle \int \frac{x^2d\,x}{\sqrt{1-x^2}}=\frac{1}{2}\sin^{-1}x-\frac{1}{2}x\sqrt{1-x^2}+C\)

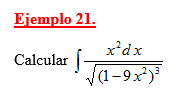
Valoraciones
No hay valoraciones aún.