Fundamentos teóricos

Descripción

Resonancia.

Para amortiguamiento pequeño, la amplitud es grande cuando la frecuencia de la fuerza impulsora está cerca de la frecuencia natural de oscilación, o cuando ω ≈ ω₀. El dramático aumento en amplitud cerca de la frecuencia natural se llama resonancia, y la frecuencia natural ω₀ también se llama la frecuencia de resonancia del sistema.

La explicación para oscilaciones de gran amplitud en la frecuencia de resonancia es que la energía se transfiere al sistema bajo las condiciones más favorables.

La figura es una gráfica de la amplitud como función de la frecuencia para un oscilador forzado con y sin amortiguamiento. Advierta que la amplitud aumenta con amortiguamiento decreciente (β → 0) y que la curva de resonancia se ensancha a medida que aumenta el amortiguamiento. En ausencia de una fuerza de amortiguamiento (β = 0), se ve por la ecuación 2 que la amplitud en estado estacionario tiende a infinito conforme ω tiende a ω₀. En otras palabras, si no hay perdidas en el sistema y se continua impulsando un oscilador inicialmente sin movimiento con una fuerza periódica que está en fase con la velocidad, la amplitud del movimiento se acumula sin límite (véase la curva café de la figura). Esta acumulación sin límite no se presenta en la práctica porque en realidad siempre hay presente algún amortiguamiento.

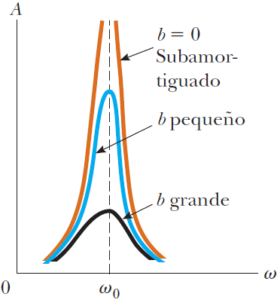
Grafica de amplitud en función de la frecuencia para un oscilador amortiguado cuando esta presente una fuerza impulsora periódica. Cuando la frecuencia ω de la fuerza impulsora es igual a la frecuencia natural ω₀ del oscilador, presenta resonancia. Advierta que la forma de la curva de resonancia depende del tamaño del coeficiente de amortiguamiento b.

Más adelante en este libro se verá que la resonancia aparece en otras áreas de la física. Por ejemplo, ciertos circuitos eléctricos tienen frecuencias naturales. Un puente tiene frecuencias naturales que se pueden poner en resonancia mediante una fuerza impulsora adecuada. Un ejemplo dramático de tal resonancia se presentó en 1940, cuando el puente Tacoma Narrows, en el estado de Washington, fue destruido por vibraciones resonantes. Aunque los vientos no eran particularmente intensos en dicha ocasión, el “aleteo” del viento a través del camino (piense en el “aleteo” de una bandera frente a un viento fuerte) proporcionó una fuerza impulsora periódica cuya frecuencia emparejo con la del puente. Las oscilaciones del puente resultantes hicieron que a final de cuentas colapsara (figura) porque el diseño del puente tenia características inadecuadas de seguridad interna.

a) En 1940 vientos turbulentos establecieron vibraciones de torsión en el puente Tacoma Narrows, haciendo que oscilara a una frecuencia cercana a una de las frecuencias naturales de la estructura del puente. b) Una vez establecida, esta condición de resonancia condujo al colapso del puente. (UPI/Bettmann Newsphotos)

Muchos otros ejemplos de vibraciones resonantes se pueden citar. Una vibración resonante que puede haber experimentado el lector es el “canturreo” de los cables de teléfono en el viento. Las maquinas se rompen con frecuencia si una parte en vibración esta

en resonancia con alguna otra parte móvil. Se ha sabido de soldados que, al marchar en cadencia por un puente, establecieron vibraciones resonantes en la estructura y por ello causaron su colapso. Siempre que cualquier sistema fìsico real sea impulsado cerca de su frecuencia de resonancia, es posible esperar oscilaciones de amplitudes muy grandes.

Quizás el ejemplo más familiar de resonancia sea lo que sucede cuando sintonizamos una radio a una estación radioemisora. Todas las estaciones radioemisoras están produciendo todo el tiempo oscilaciones forzadas en el circuito del receptor. Pero, para cada posición del sintonizador, corresponde una frecuencia natural de oscilación del circuito eléctrico del receptor. Cuando esta frecuencia coincide con aquella de la radio emisora, la energía de absorción está al máximo, y por ellos es la única estación que podemos oir. Si dos estaciones tienen frecuencias muy próximas, algunas veces las oímos simultáneamente, lo que da lugar a un efecto de interferencia.