Descripción
Par ordenado.
Un par ordenado es una pareja de objetos matemáticos, en la que se distingue un elemento y otro. El par ordenado cuyo primer elemento (o primera componente) es a y cuyo segundo elemento (o segunda componente) es b se denota como ( a , b ). En un par ordenado el orden de estos elementos es también parte de su definición y por lo tanto un par ordenado, por ejemplo ( 5 , 3 ) es distinto del par ( 3 , 5 ).
Las relaciones (y funciones) pueden ser escritas en forma de un conjunto de pares ordenados ( a , b ), donde a es un elemento perteneciente al conjunto A, y b la imagen correspondiente a dicho elemento en el conjunto B. Estos pares ordenados pueden ser analizados para determinar si una relación dada corresponde o no a una función.
En la figura:
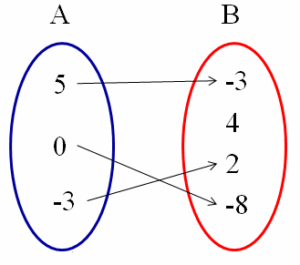
puede escribirse: R = { ( 5 , – 3 ) , ( 0 , – 8 ) , ( – 3 , 2 ) }
Los elementos del conjunto A (5, 0 y – 3) están en la primera componente de los pares ordenados, mientras que los elementos del conjunto B (– 3, 2 y – 8) están en la segunda componente. Como ya sabemos, se trata de una función, y en este caso se identifica puesto que no se repite la primera componente en dos pares ordenados distintos.
El dominio de la función está determinado por el conjunto formado por las primeras componentes, Dom f = { 5 , 0 , – 3 } y el rango por el conjunto formado por las segundas componentes, Rgo f = { – 3 , – 8 , 2 }.
Para la relación:
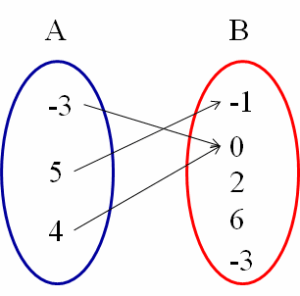
R = { ( – 3 , 0 ) , ( 5 , – 1 ) , ( 4 , 0 ) }
No se repite la primera componente en dos pares ordenados distintos, por lo tanto se trata de una función.
Se repite la segunda componente (el cero) en dos pares ordenados distintos, sin embargo, esta segunda componente no es condicional para considerar a la relación dada como función o no.
Dominio de la función: Dom f = { – 3 , 5 , 4 }.
Rango de la función: Rgo f = { – 1 , 0 }.
Para la relación:
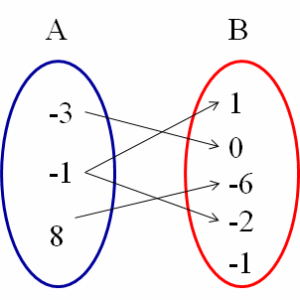
A partir del diagrama de Venn observamos que la relación no es una función, puesto que a un elemento del conjunto de partida (-1), le corresponden dos elementos en el conjunto de llegada (1 y -2). Analicemos ahora la misma relación vista como un conjunto de pares ordenados.
R = { ( – 3 , 0 ) , ( – 1 , 1 ) , ( – 1 , – 2 ) , ( 8 , – 6 ) }
El elemento “– 1” se repite en la primera componente de dos pares ordenados distintos, por lo tanto la relación dada no es una función.
Dominio de la relación: Dom R = { – 3 , – 1 , 8 }.
Rango de la relación: Rgo R = { 1 , 0 , – 6 , – 2 }.
En base a los conocimientos anteriores, podemos considerar una función como un conjunto de pares ordenados de números ( x , y ) en los que no existen dos pares ordenados diferentes con el mismo primer número. El conjunto de todos los valores admisibles de x se denomina dominio de la función, y el conjunto de todos los valores resultantes de y recibe el nombre de rango de la función.
Cuando una relación escrita mediante diagramas de Venn se escribe en la forma de pares ordenados, sólo se ilustrarán los elementos contenidos en el diagrama de Venn que pertenezcan al dominio y al rango de la relación (o función), descartándose aquellos que no tienen imagen o contraimagen. Esto puede traer algunas consecuencias y es que alguna relación que no resultare función debido a que no se cumple la condición de existencia (y si la de unicidad) cuando es escrita mediante diagramas de Venn, al escribirla en forma de pares ordenados se tendría como conclusión que si es una función. De tal manera que en este caso es necesario mostrar ambos.
Como ejemplo, la relación:
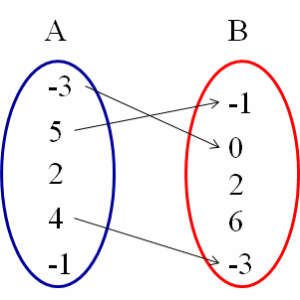
Se escribe como: R = { ( – 3 , 0 ) , ( 5 , – 1 ) , ( 4 , – 3 ) }. Según el diagrama de Venn, la relación no se trata de una función, pero según el conjunto de pares ordenados, la relación si es una función. Debe hacerse la salvedad entonces que el conjunto de pares ordenados no corresponde a una función puesto que no se ha cumplido la condición de existencia, esto es:
R = { ( – 3 , 0 ) , ( 5 , – 1 ) , ( 2 , ∄ ) , ( 4 , – 3 ) , ( – 1 , ∄ ) }
En la notación anterior ilustramos que no existe imagen para los elementos 2 y – 1 del conjunto de partida, con lo cual podemos darnos cuenta inmediatamente que no se cumple la condición de existencia, y por lo tanto el conjunto de pares ordenados no representa a una función.
Esta dificultad no ocurre cuando la relación no resulta en función debido a que no se cumple la condición de unicidad, puesto que en ese caso en el diagrama de Venn se observa que la relación no es función y también esa situación es reflejada en el conjunto de pares ordenados.
Valoraciones
No hay valoraciones aún.