Descripción
Definición de función.
Una función puede considerarse como una correspondencia de un conjunto X de números reales x a un conjunto Y de números reales y, donde el número y es único para cada valor específico de x.
Formalmente, se define una función como una relación en la cual a cada elemento del conjunto de partida X (dominio) le corresponde como imagen sólo un elemento en el conjunto de llegada Y (codominio, rango o recorrido). En la definición anterior están indicadas dos condiciones:
– Condición de existencia: todos los elementos de X están relacionados con elementos de Y, es decir, ∀ x ∈ X, ∃ y ∈ Y / ( x , y ) ∈ f.
– Condición de unicidad: cada elemento de X está relacionado con un único elemento de Y, es decir, si ( x , y1 ) ∈ f ∧ ( x , y2 ) ∈ f ⇒ y1 = y2.
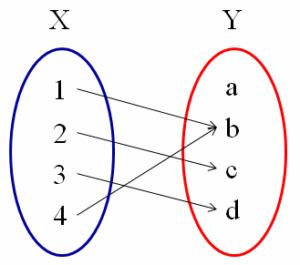
Función de X en Y : la condición de existencia asegura que de cada elemento sale alguna flecha y la de unicidad que sólo sale una.
Por definición, si a un valor “x” le corresponde una única imagen “y”, entonces la relación y = f (x) representa una función.
Dominio de una función.
En álgebra, el dominio de una función f (x)[1] es el conjunto de valores que puede tomar la variable independiente x. La colección de todos los valores que toma la variable independiente “x” se llama dominio de la función.
Cuando se usan ecuaciones para describir funciones, el dominio queda a veces claramente definido. Otras veces el dominio está implícito. Es posible que la naturaleza física del problema restrinja el dominio a un cierto subconjunto de los números reales.
Rango[2] de una función.
En álgebra, el rango de una función f (x) es el conjunto de valores que puede tomar f (x) para todos los valores posibles de x.
La colección de todos los valores que toma la variable dependiente “y” se llama rango o recorrido de la función.
La definición de función se puede ilustrar de varias formas:
Diagramas de Venn.
Sean A y B dos conjuntos no vacíos. Se denomina relación de A en B a toda proposición que permite asociar elementos del conjunto A con elementos del conjunto B.
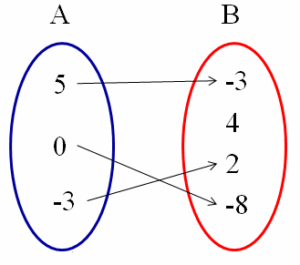
Ejemplo de función.
Si A y B están relacionados como se ilustra en la figura, entonces se tiene una relación entre A y B. Dicha relación será una función si y sólo si a cada elemento del conjunto A le corresponde un único elemento del conjunto B, esto es, no hay un elemento de A al cual le corresponden dos o más elementos de B. Adicionalmente, cada elemento de A debe tener su imagen correspondiente en B. Como ejemplo, la relación representada en la figura corresponde a una función. El conjunto de los números x pertenecientes al conjunto A que tienen imagen en B es el dominio de la función, por tanto Dom f = { – 3 , 0 , 5 } y el conjunto de números y pertenecientes al conjunto B y asignados a los valores de x en A es el rango o recorrido de la función, esto es Rgo f = { – 8 , – 3 , 2 }.
[1] La notación f (x), denominada valor de función, se debe al matemático y físico suizo Leonhard Euler (1707 – 1783).
[2] Nombre muy empleado en cálculo. Otros nombres para este conjunto son: recorrido (poco empleado en cálculo); ámbito (término muy reciente para este concepto); imagen (muy empleado en álgebra y teoría de conjuntos) y contradominio.

Valoraciones
No hay valoraciones aún.