Descripción
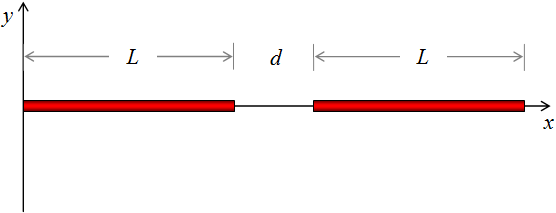
Fuerza entre varillas cargadas. Dos cargas lineales uniformes e iguales de longitud L están situadas sobre el eje x separadas una distancia d como indica la figura. (a) ¿Cuál es la fuerza que una carga lineal ejerce sobre la otra? b) Demostrar que cuando d >> L, la fuerza tiende al resultado esperado \( \displaystyle F=\frac{k\,(\lambda\,L)^2}{d^2}\).
Referencia:
Ejemplo 2.8 del Córdova. Página 57.
SOLUCIÓN DEL EJERCICIO.
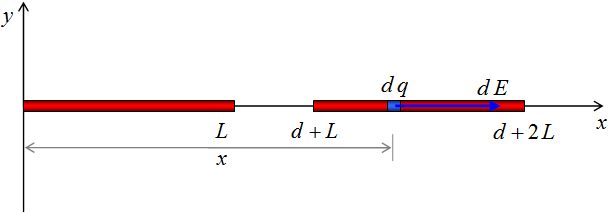
a) Se considera un elemento diferencial de carga (d q) sobre la varilla de la derecha a una distancia x con respecto al eje y. La influencia que ejerce la barra izquierda sobre dicho elemento es de repulsión, con un diferencial de campo eléctrico d E (orientado hacia la parte positiva del eje x).
Aplicando el resultado de un ejercicio precedente:
\( \displaystyle \mathbf{E}=-\frac{k\,\lambda\,L}{a\,(a+L)}\mathbf{i}\) (1)
En nuestro caso:
\( \displaystyle \mathbf{E}=-\frac{k\,\lambda\,L}{d\,(d+L)}\mathbf{i}\) (2)
En la figura se observa que d, la distancia de separación entre el extremo de la varilla izquierda y el elemento diferencial de la varilla derecha es: d = x – L. Al reemplazar en la ecuación (2):
\( \displaystyle E=\frac{k\,\lambda\,L}{(x-L)\,(x-L+L)}\)
\( \displaystyle E=\frac{k\,\lambda\,L}{(x-L)\,x}\)
\( \displaystyle E=\frac{k\,\lambda\,L}{x\,(x-L)}\) (3)
Fuerza eléctrica.
d F = E d q (4)
Al sustituir la ecuación (3) en la ecuación (4):
\( \displaystyle d\,F=\frac{k\,\lambda\,L}{x\,(x-L)}d\,q\) (5)
Para una varilla diferencial, la fracción de la carga es
d q = λ d x (6)
Al sustituir la ecuación (6) en la ecuación (5):
\( \displaystyle d\,F=\frac{k\,\lambda\,L}{x\,(x-L)}(\lambda\,d\,x)\)
\( \displaystyle d\,F=k\,\lambda^2L\left[\frac{d\,x}{x\,(x-L)}\right]\)
Integrando ambos miembros de la ecuación anterior:
\( \displaystyle \int d\,F=\int k\,\lambda^2L\left[\frac{d\,x}{x\,(x-L)}\right]\)
\( \displaystyle F=k\,\lambda^2L\int \frac{d\,x}{x\,(x-L)}\)
Límites de integración.
Para hacer el recorrido de la varilla derecha, la posición del elemento diferencial debe variar desde x = d + L (El extremo izquierdo de la varilla derecha) hasta x = d + 2 L (El extremo derecho de la varilla derecha).
\( \displaystyle F=k\,\lambda^2L\int_{d+L}^{d+2\,L} \frac{d\,x}{x\,(x-L)}\) (7)
Aplicando separación en fracciones parciales:
\( \displaystyle \frac{1}{x\,(x-L)} =\frac{A}{x}+\frac{B}{x-L} \) (8)
1 = A (x – L) + B x
Sea x = 0:
1 = A (0 – L) + B (0)
1 = A (– L)
1 = – L A
\( \displaystyle A=-\frac{1}{L}\)
Sea x = L:
1 = A (L – L) + B (L)
1 = A (0) + B L
1 = L B
\( \displaystyle B=\frac{1}{L}\)
Al sustituir las constantes A y B en la ecuación (8):
\( \displaystyle \frac{1}{x\,(x-L)} =\frac{-\frac{1}{L}}{x}+\frac{\frac{1}{L}}{x-L} \)
\( \displaystyle \frac{1}{x\,(x-L)} =-\frac{\frac{1}{L}}{x}+\frac{\frac{1}{L}}{x-L} \)
Al integrar ambos miembros de la ecuación anterior:
\( \displaystyle \int_{d+L}^{d+2\,L}\frac{1}{x\,(x-L)} =\int_{d+L}^{d+2\,L}\left(-\frac{\frac{1}{L}}{x}+\frac{\frac{1}{L}}{x-L}\right) \)
\( \displaystyle \int_{d+L}^{d+2\,L}\frac{1}{x\,(x-L)} =\frac{1}{L}\int_{d+L}^{d+2\,L}\left(-\frac{1}{x}+\frac{1}{x-L}\right) \)
La integración conduce a:
\( \displaystyle \frac{1}{x\,(x-L)} =\frac{1}{L}[-\ln x+\ln (x-L)]\bigg\vert_{d+L}^{d+2\,L} \)
\( \displaystyle \frac{1}{x\,(x-L)} =\frac{1}{L}\ln \left(\frac{x-L}{x}\right)\bigg\vert_{d+L}^{d+2\,L} \)
Aplicando el teorema fundamental del cálculo:
\( \displaystyle \frac{1}{x\,(x-L)} =\frac{1}{L}\left[\ln \left(\frac{d+2\,L-L}{d+2\,L}\right)-\ln \left(\frac{d+L-L}{d+L}\right)\right] \)
\( \displaystyle \frac{1}{x\,(x-L)} =\frac{1}{L}\left[\ln \left(\frac{d+L}{d+2\,L}\right)-\ln \left(\frac{d}{d+L}\right)\right] \)
\( \displaystyle \frac{1}{x\,(x-L)} =\frac{1}{L}\ln \left(\frac{\frac{d+L}{d+2\,L}}{\frac{d}{d+L}}\right) \)
\( \displaystyle \frac{1}{x\,(x-L)} =\frac{1}{L}\ln\left[\frac{(d+L)^2}{d\,(d+2\,L)}\right] \)
Al sustituir la expresión anterior en la ecuación (7):
\( \displaystyle F=k\,\lambda^2L\left[\frac{1}{L}\ln\left[\frac{(d+L)^2}{d\,(d+2\,L)}\right]\right]\)
\( \displaystyle F=k\,\lambda^2\ln\left[\frac{(d+L)^2}{d\,(d+2\,L)}\right]\) (9)
b) Puede demostrarse aplicando la Regla de L´Hopital, que si L → 0, entonces la fuerza resultante entre las dos varillas es \( \displaystyle F=\frac{k\,Q^2}{d^2}\), la cual es equivalente a la fuerza entre dos cargas puntuales Q separadas una distancia d.
Demostración.
\( \displaystyle F=k\,\lambda^2\ln\left[\frac{(d+L)^2}{d\,(d+2\,L)}\right]\) (9)
Siendo λ = Q/L, la fuerza eléctrica entre las dos varillas (Ecuación 9) puede escribirse en la forma:
\( \displaystyle F=k\,\left(\frac{Q}{L}\right)^2\ln\left[\frac{(d+L)^2}{d\,(d+2\,L)}\right]\) (10)
Al aplicar las propiedades de los logaritmos:
\( \displaystyle F=k\,\left(\frac{Q}{L}\right)^2\{\ln\,(d+L)^2-\ln\,[d\,(d+2\,L)]\}\)
\( \displaystyle F=\frac{k\,Q^2}{L^2}[2\,\ln\,(d+L)-\ln d-\ln\,(d+2\,L)]\)
\( \displaystyle F=k\,Q^2\left[\frac{2\,\ln\,(d+L)-\ln d-\ln\,(d+2\,L)}{L^2}\right]\)
Al tomar el límite cuando L → 0:
\( \displaystyle F=k\,Q^2\lim_{L \to 0}\left[\frac{2\,\ln\,(d+L)-\ln d-\ln\,(d+2\,L)}{L^2}\right]\)
La evaluación del límite anterior conduce a una forma indeterminada 0/0. Se aplica la regla de L´Hopital derivando tanto el numerador como el denominador en función de L.
\( \displaystyle F=k\,Q^2\lim_{L \to 0}\left(\frac{\frac{2}{d+L}-\frac{2}{d+2\,L}}{2\,L}\right)\)
\( \displaystyle F=k\,Q^2\lim_{L \to 0}\left[\frac{\frac{2\,(d+2\,L)-2\,(d+L)}{(d+L)\,(d+2\,L)}}{2\,L}\right]\)
\( \displaystyle F=k\,Q^2\lim_{L \to 0}\left[\frac{\frac{2\,d+4\,L-2\,d-2\,L}{(d+L)\,(d+2\,L)}}{2\,L}\right]\)
\( \displaystyle F=k\,Q^2\lim_{L \to 0}\left[\frac{\frac{2\,L}{(d+L)\,(d+2\,L)}}{2\,L}\right]\)
\( \displaystyle F=k\,Q^2\lim_{L \to 0}\left[\frac{1}{(d+L)\,(d+2\,L)}\right]\)
Al evaluar el límite:
\( \displaystyle F=k\,Q^2\left(\frac{1}{d^2}\right)\)
\( \displaystyle F=\frac{k\,Q^2}{d^2}\) (11)
Carga total de una varilla:
Q = λ L (12)
Al sustituir la ecuación (12) en la ecuación (11):
\( \displaystyle F=\frac{k\,(\lambda\,L)^2}{d^2}\) (13)




Valoraciones
No hay valoraciones aún.