Descripción
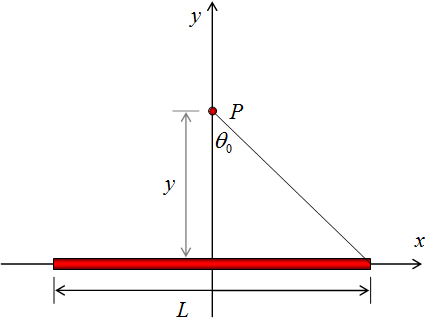
Una línea de carga uniforme. Una varilla cargada de longitud L que presenta una densidad uniforme de carga lineal positiva λ = q / L, donde q es la carga total transportada por la varilla. Encontrar el campo en el punto P a una distancia y de la varilla en su bisector perpendicular.
Referencia:
Ejemplo Sección 26-4 del Resnick – Halliday. Quinta Edición. Página 592.
SOLUCIÓN DEL EJERCICIO.
Se considera un elemento diferencial de carga (d q) sobre la varilla a una distancia x con respecto al eje y. La influencia que ejerce dicho elemento sobre la carga de prueba colocada en el punto P es de repulsión, con un diferencial de campo eléctrico d E (orientado con un ángulo θ respecto a la vertical). d E se descompone en sus componentes rectangulares d Ex y d Ey.
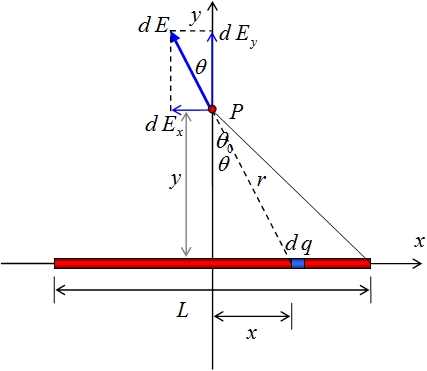
Componentes rectangulares del campo eléctrico.
Componente horizontal.
d Ex = d E sen θ
Por simetría Ex = 0
Componente vertical.
d Ey = d E cos θ (1)
Al integrar ambos miembros de la ecuación (1):
\( \displaystyle \int d\,E_y = \int d\,E\cos\,\theta\)
\( \displaystyle E_y = \int d\,E\cos\,\theta\) (2)
El diferencial del campo eléctrico viene dado por:
\( \displaystyle dE = k\frac{d\,q}{d^2} \) (3)
Al sustituir la ecuación (3) en la ecuación (2):
\( \displaystyle E_y = \int k\frac{d\,q}{d^2}\cos\theta\) (4)
Para determinar el diferencial de carga, recurrimos a la definición de densidad lineal de carga:
\( \displaystyle \lambda = \frac{q}{x}\)
Al despejar la carga:
q = λ x
Al diferenciar con respecto a la longitud x:
d q = λ d x (5)
Distancia entre el elemento diferencial de carga (d q) y la carga de prueba ubicada en el punto P.
r2 = x2 + y2 (6)
\( \displaystyle r = \sqrt{x^2+y^2} \) (7)
Ángulo que forma el diferencial de campo eléctrico (d E) con la vertical.
\( \displaystyle cos \theta = \frac{y}{r} \) (8)
Al sustituir la ecuación (7) en la ecuación (8):
\( \displaystyle cos\,\theta = \frac{y}{\sqrt{x^2+y^2}} \) (9)
Al sustituir las ecuaciones (6), (8) y (9) en la ecuación (4):
\( \displaystyle E_y = \int k\frac{\lambda\,d\,x}{x^2+y^2}\frac{y}{\sqrt{x^2+y^2}}\)
\( \displaystyle E_y = \int \frac{k\,\lambda\,y\,d\,x}{(x^2+y^2)^{\frac{3}{2}}}\)
\( \displaystyle E_y = k\,\lambda\,y\,\int \frac{d\,x}{(x^2+y^2)^{\frac{3}{2}}}\)
Límites de integración.
Para hacer el recorrido de la varilla, la posición del elemento diferencial debe variar desde \( x = -\frac{1}{2}L\) (El extremo izquierdo de la varilla) hasta \( x = \frac{1}{2}L\) (El extremo derecho de la varilla).
\( \displaystyle E_y = k\,\lambda\,y\,\int_{-\frac{1}{2}L}^{\frac{1}{2}L}\frac{d\,x}{(x^2+y^2)^{\frac{3}{2}}}\)
Por simetría.
\( \displaystyle E_y = 2\,k\,\lambda\,y\,\int_0^{\frac{1}{2}L}\frac{d\,x}{(x^2+y^2)^{\frac{3}{2}}}\) (10)
La integral se resuelve aplicando sustitución trigonométrica o mediante el uso de tabla de integrales.
Aplicando sustitución trigonométrica:
x = y tan θ (11)
d x = y sec2θ d θ (12)
x2 + y2 = y2 sec2θ (13)
Al sustituir las ecuaciones (11), (12) y (13) en la ecuación (10):
\( \displaystyle E_y = 2\,k\,\lambda\,y\,\int_0^{\theta_0}\frac{y\,\sec^2\theta\,d\,\theta}{(y^2\sec^2\theta)^{\frac{3}{2}}}\)
\( \displaystyle E_y = 2\,k\,\lambda\,y^2\int_0^{\theta_0}\frac{\sec^2\theta\,d\,\theta}{y^3\sec^3\theta}\)
\( \displaystyle E_y = \frac{2\,k\,\lambda}{y}\int_0^{\theta_0}\frac{d\,\theta}{\sec\theta}\)
\( \displaystyle E_y = \frac{2\,k\,\lambda}{y}\int_0^{\theta_0}\cos\theta\,d\,\theta\)
La integración conduce a:
\( \displaystyle E_y = \frac{2\,k\,\lambda}{y}\sin\theta\,\bigg\vert_0^{\theta_0}\)
Aplicando el teorema fundamental del cálculo:
\( \displaystyle E_y = \frac{2\,k\,\lambda}{y}\sin\theta_0-\frac{2\,k\,\lambda}{y}\sin 0\)
\( \displaystyle E_y = \frac{2\,k\,\lambda}{y}\sin\theta_0\) (14)
De la figura:
\( \displaystyle \sin\theta = \frac{\frac{1}{2}L}{\sqrt{(\frac{1}{2}L)^2+y^2}}\)
\( \displaystyle \sin\theta = \frac{\frac{1}{2}L}{\sqrt{\frac{1}{4}L^2+y^2}}\) (15)
Al sustituir la ecuación (15) en la ecuación (14):
\( \displaystyle E_y = \frac{2\,k\,\lambda}{y}\cdot\frac{\frac{1}{2}L}{\sqrt{\frac{1}{4}L^2+y^2}} \)
\( \displaystyle E_y = \frac{k\,\lambda\,L}{y\sqrt{\frac{1}{4}L^2+y^2}} \)
\( \displaystyle \mathbf{E} = \frac{k\,\lambda\,L}{y\sqrt{\frac{1}{4}L^2+y^2}} \mathbf{j}\) Unidades de campo eléctrico. (16)
Campo eléctrico en función de la carga total de la varilla.
q = λ L (17)
Al sustituir la ecuación (17) en la ecuación (16):
\( \displaystyle \mathbf{E} = \frac{k\,q}{y\sqrt{\frac{1}{4}L^2+y^2}} \mathbf{j}\) Unidades de campo eléctrico. (18)
Aplicaciones de la ecuación del campo eléctrico para una varilla.
Varilla infinita (L → ∞).
\( \displaystyle \mathbf{E} = \frac{k\,\lambda\,L}{y\sqrt{\frac{1}{4}L^2+y^2}} \mathbf{j}\) (16)
Si L → ∞, entonces \( \frac{1}{4}L^2+y^2\approx \frac{1}{4}L^2\).
\( \displaystyle \mathbf{E} = \frac{k\,\lambda\,L}{y\sqrt{\frac{1}{4}L^2}} \mathbf{j}\)
\( \displaystyle \mathbf{E} = \frac{k\,\lambda\,L}{y(\frac{1}{2}L)} \mathbf{j}\)
\( \displaystyle \mathbf{E} = \frac{2\,k\,\lambda}{y} \mathbf{j}\) Unidades de campo eléctrico. (19)
Campo eléctrico en un punto “alejado” de la varilla (y >> L).
\( \displaystyle \mathbf{E} = \frac{k\,q}{y\sqrt{\frac{1}{4}L^2+y^2}} \mathbf{j}\) (18)
Si y >> L, entonces \( \frac{1}{4}L^2+y^2\approx y^2\).
\( \displaystyle \mathbf{E} = \frac{k\,q}{y\sqrt{y^2}} \mathbf{j}\)
\( \displaystyle \mathbf{E} = \frac{k\,q}{y\,(y)} \mathbf{j}\)
\( \displaystyle \mathbf{E} = \frac{k\,q}{y^2} \mathbf{j}\)
\( \displaystyle \Vert E\Vert = \frac{k\,q}{y^2} \)
El campo eléctrico obtenido es el equivalente al campo eléctrico debido a una carga puntual cuyo valor es q a una distancia y, esto es, la varilla se comporta como una carga puntual.


Valoraciones
No hay valoraciones aún.