EJERCICIO 1

Descripción

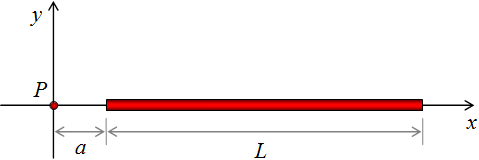
Campo eléctrico debido a una barra con carga. Una barra de longitud L tiene una carga positiva uniforme por unidad de longitud λ y una carga total Q. Calcule el campo eléctrico en un punto P que se ubica a lo largo del eje largo de la barra y a una distancia a desde un extremo.

The Electric Field Due to a Charged Rod. A rod of length L, has a uniform positive charge per unit length λ and a total charge Q. Calculate the electric field at a point P that is located along the long axis of the rod and a distance a from one end (Figure).

Referencias: 

Ejemplo 23.8 del Serway. Tercera Edición. Página 16.

Ejemplo 23.7 del Serway – Beichner. Quinta Edición. Página 724.

Example 23.7 from Serway. Sixth Edition. Page 721.

Ejemplo 23.6. Sección 23.5 del Serway – Jewett. Séptima Edición. Página 656.

Example 23.7 from Serway – Jewett. Ninth Edition. Page 705.

SOLUCIÓN DEL EJERCICIO.

Se considera un elemento diferencial de carga (d q) sobre la barra a una distancia x con respecto al eje y. La influencia que ejerce dicho elemento sobre la carga de prueba colocada en el origen es de repulsión, con un diferencial de campo eléctrico d E (orientado hacia la parte negativa del eje x).

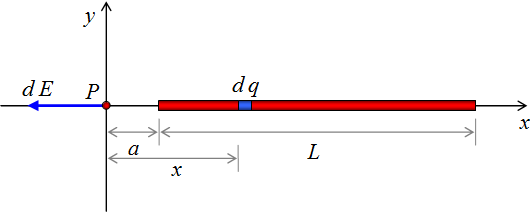
El diferencial del campo eléctrico viene dado por:

\( \displaystyle d\,E = k\frac{d\,q}{r^2}\) (1)

Al integrar ambos miembros de la ecuación (1):

\( \displaystyle \int d\,E=\int k\frac{d\,q}{r^2}\)

\( \displaystyle E=k\int \frac{d\,q}{r^2}\) (2)

Para determinar el diferencial de carga, recurrimos a la definición de densidad lineal de carga:

\( \displaystyle \lambda=\frac{q}{x}\)

Al despejar la carga:

q = λ x

Al diferenciar con respecto a la longitud x:

d q = λ d x (3)

Distancia entre el elemento diferencial de carga (d q) y la carga de prueba ubicada en el punto P.

r = x (4)

Al sustituir las ecuaciones (3) y (4) en la ecuación (2):

\( \displaystyle E=k\int \frac{\lambda\,d\,x}{x^2}\)

\( \displaystyle E=k\,\lambda\int\frac{d\,x}{x^2}\)

Límites de integración.

Para hacer el recorrido de la varilla, la posición del elemento diferencial debe variar desde x = a (El extremo izquierdo de la varilla) hasta x = a + L (El extremo derecho de la varilla).

\( \displaystyle E=k\,\lambda\int_a^{a+L}\frac{d\,x}{x^2}\)

La integración conduce a:

\( \displaystyle E=k\,\lambda\left(-\frac{1}{x}\bigg\vert_a^{a+L}\right)\)

Al aplicar el teorema fundamental del cálculo:

\( \displaystyle E=k\,\lambda\left(-\frac{1}{a+L}+\frac{1}{a}\right)\)

\( \displaystyle E=k\,\lambda\left[\frac{-a+a+L}{a\,(a+L)}\right]\)

\( \displaystyle E=k\,\lambda\left[\frac{L}{a\,(a+L)}\right]\)

\( \displaystyle E=\frac{k\,\lambda\,L}{a\,(a+L)}\)

\( \displaystyle \mathbf{E}=-\frac{k\,\lambda\,L}{a\,(a+L)}\mathbf{i}\) Unidades de campo  eléctrico. (5)

Campo eléctrico en función de la carga total de la varilla.

\( \displaystyle \lambda=\frac{Q}{L}\) (6)

Al sustituir la ecuación (6) en la ecuación (5):

\( \displaystyle  \mathbf{E}=-\frac{k\,\left(\frac{Q}{L}\right)\,L}{a\,(a+L)}\mathbf{i}\)

\( \displaystyle \mathbf{E}=-\frac{k\,Q}{a\,(a+L)}\mathbf{i}\) Unidades de campo eléctrico. (7)

Aplicaciones de la ecuación del campo eléctrico para una varilla.

Varilla infinita (L → ∞).

\( \displaystyle \mathbf{E}=-\frac{k\,\lambda\,L}{a\,(a+L)}\mathbf{i}\) (5)

Si L → ∞, entonces a + L ≈ L.

\( \displaystyle \mathbf{E}=-\frac{k\,\lambda\,L}{a\,L}\mathbf{i}\)

\( \displaystyle \mathbf{E}=-\frac{k\,\lambda}{a}\mathbf{i}\) Unidades de campo eléctrico. (8)

Campo eléctrico en un punto “alejado” del extremo izquierdo de la varilla (a >> L).

\( \displaystyle \mathbf{E}=-\frac{k\,Q}{a\,(a+L)}\mathbf{i}\) (7)

Si a >> L, entonces a + L ≈ a.

\( \displaystyle \mathbf{E}=-\frac{k\,Q}{a\,(a)}\mathbf{i}\)

\( \displaystyle \mathbf{E}=-\frac{k\,Q}{a^2}\mathbf{i}\)

\( \displaystyle \Vert \mathbf{E}\Vert=\frac{k\,Q}{a^2}\) Unidades de campo eléctrico.

El campo eléctrico obtenido es el equivalente al campo eléctrico debido a una carga puntual cuyo valor es Q a una distancia a, esto es, la varilla se comporta como una carga puntual.