Descripción
Calcular \( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}\)
Referencias:
Ejemplo 114 del Filippis. Página 289.
Ejemplo 6.2 del Cortés. Octava Edición. Página 167.
SOLUCIÓN DEL EJERCICIO.
El integrando tiene la forma \( \displaystyle\sqrt{a^2-u^2}\), se hace la sustitución:
x = 5 sen θ
d x = 5 cos θ d θ
\( \displaystyle\sqrt{25 – x^2} = \sqrt{25 – (5 \sin \theta)^2} \)
\(\displaystyle\sqrt{25 – x^2}= \sqrt{25 – 25 \sin^2 \theta} \)
\(\displaystyle\sqrt{25 – x^2}= \sqrt{25\,(1 – \sin^2 \theta)} \)
\(\displaystyle\sqrt{25 – x^2}= \sqrt{25\,\cos^2 \theta} \)
\(\displaystyle\sqrt{25 – x^2}= 5 \cos \theta \)
Al sustituir \( \displaystyle\sqrt{25-x^2}=5\,\cos\theta\), d x = 5 cos θ d θ y x = 5 sen θ en la integral:
\( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}=\int\frac{(5\,\cos\theta)\,(5\,\cos \theta\,d\,\theta)}{5 \sin \theta}\)
\( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}=\int\frac{25\,\cos^2\theta\,d\,\theta}{5\sin\theta}\)
Al simplificar los valores numéricos:
\( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}=\int\frac{5\,\cos^2\theta\,d\,\theta}{\sin\theta}\)
\( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}=5\int\frac{\cos^2\theta\,d\,\theta}{\sin\theta}\)
\( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}=5\int\frac{(1-\sin^2\theta)\,d\,\theta}{\sin\theta}\)
Al separar términos en el integrando:
\( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}=5\int \left(\frac{1}{\sin\theta}-\frac{\sin^2\theta}{\sin\theta}\right)\,d\,\theta\)
\( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}=5\int (\csc\theta-\sin\theta)\,d\,\theta\)
\( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}=5\int \csc\theta\,d\,\theta-5\int\sin\theta\,d\,\theta\)
La integración conduce a:
\( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}=5\ln\,(\csc\theta-\cot\theta)-5(-\cos\theta)+C\)
\( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}=5\ln\,(\csc\theta-\cot\theta)+5\cos\theta+C\) (1)
Para volver a la variable original se debe definir csc θ, cot θ y cos θ en función de x.
Partiendo de la sustitución trigonométrica realizada:
x = 5 sen θ
\( \displaystyle \sin\theta=\frac{x}{5}=\frac{\text{Cateto opuesto}}{\text{Hipotenusa}}\)
Se construye un triángulo rectángulo cuyo cateto opuesto es x e hipotenusa es 5. El lado faltante, se determina con la aplicación del teorema de Pitágoras.
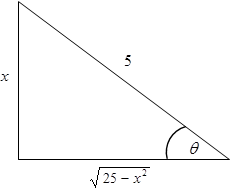
Observe que la magnitud del lado faltante coincide con la expresión \( \displaystyle\sqrt{25-x^2}\) que se encuentra en el integrando.
A partir del triángulo obtenido, se define csc θ, cot θ y cos θ
\( \displaystyle \csc\theta=\frac{\text{Hipotenusa}}{\text{Cateto opuesto}}\)
\( \displaystyle \csc\theta=\frac{5}{x}\)
\( \displaystyle \cot\theta=\frac{\text{Cateto adyacente}}{\text{Cateto opuesto}}\)
\( \displaystyle \cot\theta=\frac{\sqrt{25-x^2}}{x}\)
\( \displaystyle \cos\theta=\frac{\text{Cateto adyacente}}{\text{Hipotenusa}}\)
\( \displaystyle \cos\theta=\frac{\sqrt{25-x^2}}{5}\)
Al sustituir en la Ecuación (1):
\( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}=5\ln\,\left(\frac{5}{x}-\frac{\sqrt{25-x^2}}{x}\right)+5\left(\frac{\sqrt{25-x^2}}{5}\right)+C\)
\( \displaystyle \int\frac{\sqrt{25-x^2}\,d\,x}{x}=5\ln\,\left(\frac{5-\sqrt{25-x^2}}{x}\right)+5\sqrt{25-x^2}+C\)