Descripción
Función lineal.
Definición de la función lineal.
La función lineal se define por:
y = f (x) = m x + b m ≠ 0 m, b ∈ ℝ m, b = Constantes.
Los parámetros m y b representan la pendiente de la recta y el corte al eje “y” u ordenada en el origen respectivamente.
Ejemplos de la función lineal.
Son ejemplos de función lineal, junto con el valor de la pendiente y el corte al eje “y” los siguientes:
f (x) = 3 x – 2 m = 3, b = – 2
f (x) = – 4 x + 5 m = – 4, b = 5
f (x) = 6 – 3 x m = – 3, b = 6
f (x) = 2 x m = 2, b = 0
\( f\,(x) = \frac{3}{2}x+7\) \( m = \frac{3}{2}\) , b = 7
\( f\,(x) = \frac{5}{3}-\frac{1}{7}x\) \( m = -\frac{1}{7}\), \(b = \frac{5}{3}\)
Dominio de la función lineal.
El dominio de la función está conformado por el conjunto de valores que adopta la variable independiente (x). En este caso, x puede adoptar cualquier valor real.
Dom f = ℝ
De acuerdo a la forma algebraica de la función lineal, su dominio es el campo de los números reales (ℝ), sin embargo, el problema puede plantearse restringiendo éste a un intervalo. Cuando eso ocurre se dice que la función lineal tiene el dominio restringido y el dominio de la función es el intervalo indicado. El estudio de la función se realiza en el campo de los números reales y finalmente se hacen los ajustes para enmarcar la gráfica en el dominio (restringido) indicado para la función.
El concepto discutido en el párrafo anterior acerca del dominio restringido de una función es particularmente útil cuando se estudian funciones ramificadas, las cuales forman parte de esta unidad del curso de cálculo diferencial.
Gráfica de la función lineal.
La representación gráfica de la función lineal es una recta cuya inclinación depende del valor de “m”:
Se tienen los dos casos:
|
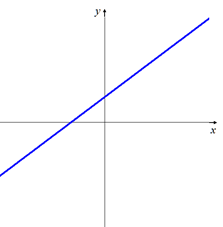
Coeficiente de x positivo: m > 0 Recta creciente. |
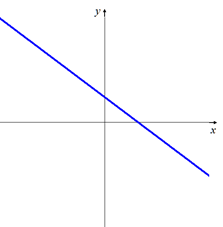
Coeficiente de x negativo: m < 0 Recta decreciente. |
Puntos notables de la gráfica de la función lineal.
Estos son los puntos suficientes para realizar la gráfica de la función. Cuando sea necesario, se deben tomar puntos adicionales mediante la sustitución apropiada de valores de x en la función.
Puntos de intersección con los ejes.
Intersección con el eje y: x = 0.
Coordenadas del punto de intersección con el eje y.
Al sustituir x = 0 en la función lineal:
y = m (0) + b
y = b
Corte al eje “y”: ( 0 , b )
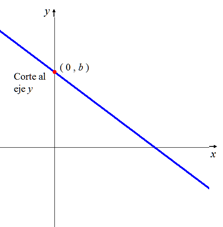
Independientemente de si la recta es creciente o decreciente, el corte con el eje “y” es el punto (0 , b).
Intersección con el eje x: y = 0.
Siempre es posible determinar un punto de intersección con el eje x para la función lineal. Para determinarlos e necesario resolver la ecuación de primer grado 0 = m x + b.
m x + b = 0
m x = – b
\( \displaystyle x = -\frac{b}{m}\)
Corte al eje x: \( \displaystyle x = \left(-\frac{b}{m},0\right)\)
Función identidad.
La función lineal particular definida por f (x) = x se denomina función identidad. Su gráfica, dibujada en la figura, es la recta que bisecta los cuadrantes primero y tercero.
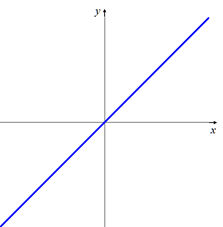
Función identidad.
Consideraciones adicionales.
1) Si la función tiene dominio restringido, se deben considerar los extremos del intervalo que restringen al dominio. Esto es, evaluar la función en los extremos, con excepción de + ∞ ó – ∞.
2) Es posible que la función lineal resulte de la simplificación de factores en una función racional. En ese caso se debe hacer la simplificación, determinar el dominio (como una función racional) y hacer el análisis de la función lineal resultante. Se debe tener cuidado de excluir de la gráfica de la función los puntos correspondientes a valores de x que anulen el denominador de la función racional original (si los hubiere).
Rango de la función lineal.
Rgo f = ℝ
Cuando la función lineal tiene el dominio restringido, el rango también estará restringido a un intervalo. Se debe evaluar la función en los extremos del intervalo del dominio y determinar los correspondientes valores de “y” que delimitan el rango de la función.
Valoraciones
No hay valoraciones aún.