EJERCICIO 1

Descripción

Sección 2.3 del Bird. Página 2-10.

Flujo a través de un tubo circular. Consideremos el flujo laminar en estado estacionario de un fluido de densidad constante ρ en un tubo <<muy largo>> de longitud L y radio R.

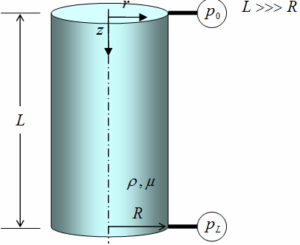
Determinar:

a) Distribución de la densidad de flujo de cantidad de movimiento.

b) Distribución de velocidad.

c) Velocidad máxima.

d) Velocidad media.

e) Velocidad volumétrica de flujo.

f) Componente de la fuerza F del fluido sobre la superficie.

SOLUCIÓN DEL EJERCICIO.

Condiciones:

Estado estacionario.

Flujo laminar.

Propiedades del fluido constantes (ρ, μ).

Fluido Newtoniano.

Efectos de borde despreciables.

Flujo longitudinal (en dirección z): v_r = 0, v_θ = 0, v_z ≠ 0.

La velocidad varía en función de r: v_z = v_z (r).

Balance de cantidad de movimiento.

2 π r L τ_rz | _r – 2 π r L τ_rz | _{r + ∆ r} + 2 π r ∆ r L ρ g_z + 2 π r ∆ r (p₀ – p_L) = 0

g_z es la componente gravitacional en la dirección del flujo. En este caso g_z = g.

2 π r L τ_rz | _r – 2 π r L τ_rz | _{r + ∆ r} + 2 π r ∆ r L ρ g + 2 π r ∆ r (p₀ – p_L) = 0 (1)

Al dividir entre 2 π L:

\( \displaystyle r\,\tau_{rz} \big|_{r} – r\,\tau_{rz} \big|_{r + \Delta\,r}  + r\,\Delta\,r \,\rho\,g + r\,\Delta\,r \frac{(p_{0} – p_{L})}{L} = 0 \)

\( \displaystyle r\,\tau_{rz} \big|_{r} – r\,\tau_{rz} \big|_{r + \Delta\,r}  + \left(\rho\,g + \frac{p_{0} – p_{L}}{L}\right) r\,\Delta\,r = 0 \)

Sea \( \displaystyle \rho\,g + \frac{p_{0} – p_{L}}{L} = \frac{P_0-P_L}{L} \)

\( \displaystyle r\,\tau_{rz} \big|_{r} – r\,\tau_{rz} \big|_{r + \Delta\,r}  + \left( \frac{P_{0} – P_{L}}{L}\right) r\,\Delta\,r = 0 \)

\( \displaystyle r\,\tau_{rz} \big|_{r} – r\,\tau_{rz} \big|_{r + \Delta\,r} =-  \left( \frac{P_{0} – P_{L}}{L}\right) r\,\Delta\,r \)

Al multiplicar por (– 1) la ecuación anterior:

\( \displaystyle r\,\tau_{rz} \big|_{r + \Delta\,r} – r\,\tau_{rz} \big|_{r} = \left( \frac{P_{0} – P_{L}}{L}\right) r\,\Delta\,r \)

\( \displaystyle \frac{r\,\tau_{rz} \big|_{r + \Delta\,r} – r\,\tau_{rz} \big|_{r}}{\Delta\,r} = \left( \frac{P_{0} – P_{L}}{L}\right) r \)

Tomando el límite cuando ∆ r → 0 en la ecuación anterior:

\( \displaystyle \lim_{\Delta\,r \to 0}\frac{r\,\tau_{rz} \big|_{r + \Delta\,r} – r\,\tau_{rz} \big|_{r}}{\Delta\,r} = \lim_{\Delta\,r \to 0} \left( \frac{P_{0} – P_{L}}{L}\right) r \)

\( \displaystyle \lim_{\Delta\,r \to 0}\frac{r\,\tau_{rz} \big|_{r + \Delta\,r} – r\,\tau_{rz} \big|_{r}}{\Delta\,r} = \left( \frac{P_{0} – P_{L}}{L}\right) r \)

Aplicando la definición de derivada:

\( \displaystyle \frac{d}{d\,r}(r\,\tau_{rz})=\left(\frac{P_0-P_L}{L}\right) r \)

Al separar variables en la ecuación anterior:

\( \displaystyle d\,(r\,\tau_{rz})=\left(\frac{P_0-P_L}{L}\right) r\,d\,r \)

Integrando ambos miembros de la ecuación:

\( \displaystyle \int d\,(r\,\tau_{rz})=\int \left(\frac{P_0-P_L}{L}\right) r\,d\,r \)

\( \displaystyle \int d\,(r\,\tau_{rz})=\left(\frac{P_0-P_L}{L}\right)\int r\,d\,r \)

La integración conduce a:

\( \displaystyle r\,\tau_{rz} = \left(\frac{P_0 – P_L}{L} \right) \left(\frac{r^2}{2}\right) + C_1 \)

\( \displaystyle r\,\tau_{rz} = \left( \frac{P_0 – P_L}{2\,L} \right) r^2 + C_1 \)

\( \displaystyle \tau_{rz} = \left(\frac{P_0 – P_L}{2\,L} \right) r + \frac{C_1}{r} \) (2)

Condición de borde: Para r = 0, τ_rz ≠ ∞.

C₁ = 0 (3)

Al sustituir la ecuación (3) en la ecuación (2):

\( \displaystyle \tau_{rz} = \left(\frac{P_0 – P_L}{2\,L} \right) r \) (4)

La ecuación (4) es la distribución de la densidad de flujo de cantidad de movimiento.

b) Distribución de velocidad.

Fluido Newtoniano.

\( \displaystyle \tau_{rz} = -\mu \frac{d\,v_z}{d\,r} \) (5)

Al sustituir la ecuación (5) en la ecuación (4):

\( \displaystyle -\mu \frac{d\,v_z}{d\,r} = \left(\frac{P_0 – P_L}{2\,L} \right) r \)

Al separar las variables en la ecuación anterior:

\( \displaystyle d\,v_z = -\left(\frac{P_0 – P_L}{2\,\mu\,L} \right) r\,d\,r \)

Al integrar ambos miembros de la ecuación:

\( \displaystyle \int d\,v_z = \int -\left(\frac{P_0 – P_L}{2\,\mu\,L} \right) r\,d\,r \)

\( \displaystyle \int d\,v_z = -\left(\frac{P_0 – P_L}{2\,\mu\,L} \right) \int r\,d\,r \)

La integración conduce a:

\( \displaystyle v_z = -\left(\frac{P_0 – P_L}{2\,\mu\,L} \right) \left(\frac{r^2}{2}\right) + C_2  \)

 \( \displaystyle v_z = -\left(\frac{P_0 – P_L}{4\,\mu\,L} \right) r^2 + C_2  \) (6)

Condición de borde: Para r = R, v_z = 0.

Al sustituir en la ecuación (6):

\( \displaystyle 0 = -\left(\frac{P_0 – P_L}{4\,\mu\,L} \right) (R)^2 + C_2  \)

Al despejar C₂ en la ecuación anterior:

\( \displaystyle C_2 = \left(\frac{P_0 – P_L}{4\,\mu\,L} \right) R^2 \) (7)

Al sustituir la ecuación (7) en la ecuación (6):

\( \displaystyle v_z = -\left(\frac{P_0 – P_L}{4\,\mu\,L} \right) r^2 + \left(\frac{P_0 – P_L}{4\,\mu\,L} \right) R^2  \) 

\( \displaystyle v_z = \left(\frac{P_0 – P_L}{4\,\mu\,L} \right) (R^2 – r^2)  \)

Al multiplicar y dividir por R²:

\( \displaystyle v_z = \left(\frac{P_0 – P_L}{4\,\mu\,L} \right) (R^2 – r^2)\times\frac{R^2}{R^2} \)

\( \displaystyle v_z = \frac{(P_0 – P_L)\,R^2}{4\,\mu\,L} \left( \frac{R^2 – r^2}{R^2}\right) \)

\( \displaystyle v_z = \frac{(P_0 – P_L)\,R^2}{4\,\mu\,L} \left( \frac{R^2}{R^2} – \frac{r^2}{R^2}\right) \)

\( \displaystyle v_z = \frac{(P_0 – P_L)\,R^2}{4\,\mu\,L} \left(1 – \frac{r^2}{R^2}\right) \)

\( \displaystyle v_z = \frac{(P_0 – P_L)\,R^2}{4\,\mu\,L} \left[1 – \left(\frac{r}{R}\right)^2\right] \) (8)

Distribución de velocidad parabólico.

c) Velocidad máxima.

La velocidad es máxima en r = 0.

v_z,max = v_z (0)

Al sustituir r = 0 en la ecuación (8):

\( \displaystyle v_{z,max} = \frac{(P_0 – P_L)R^2}{4 \mu L} \left[ 1 – \left(\frac{0}{R}\right)^2\right] \)

\( \displaystyle v_{z,max} = \frac{(P_0 – P_L)\,R^2}{4\,\mu\,L} \) (9)

En la figura siguiente se muestra la distribución de velocidad, la velocidad máxima y la distribución de la densidad de flujo de cantidad de movimiento.

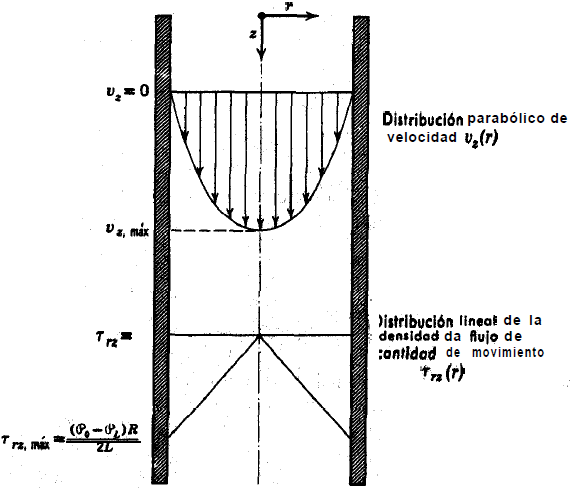
Velocidad media.

\( \displaystyle <v_z> = \displaystyle \frac{\int_0^{2\,\pi}\int_0^R v_z\,r\,d\,r\,d\, \theta}{\int_0^{2\,\pi}\int_0^R r\,d\,r\,d\,\theta} \) (10)

Al sustituir la ecuación (8) en la ecuación (10):

\( \displaystyle <v_z> = \displaystyle \frac{\int_0^{2\,\pi}\int_0^R \frac{(P_0 – P_L)\,R^2}{4\,\mu\,L} \left[ 1 – \left(\frac{r}{R}\right)^2\right] r\,d\,r\,d\,\theta}{\int_0^{2\,\pi}\int_0^R r\,d\,r\,d\,\theta} \)

\( \displaystyle <v_z> = \displaystyle \frac{\int_0^{2\,\pi}\int_0^R \frac{(P_0 – P_L)\,R^2}{4\,\mu\,L} \left( 1 – \frac{r^2}{R^2}\right) r\,d\,r\,d\,\theta}{\int_0^{2\,\pi}\int_0^R r\,d\,r\,d\,\theta} \)

\( \displaystyle <v_z> = \displaystyle \frac{\int_0^{2\,\pi}\int_0^R \frac{(P_0 – P_L)\,R^2}{4\,\mu\,L} \left( r – \frac{r^3}{R^2}\right) d\,r\,d\,\theta}{\int_0^{2\,\pi}\int_0^R r\,d\,r\,d\,\theta} \)

\( \displaystyle <v_z> = \displaystyle \frac{\frac{(P_0 – P_L)\,R^2}{4\,\mu\, L}\int_0^R \left( r – \frac{r^3}{R^2}\right) d\,r\int_0^{2\,\pi} d\,\theta}{\int_0^R r\,d\,r \int_0^{2\,\pi} d\,\theta} \)

Al simplificar : \( \displaystyle \int_0^{2\,\pi} d\,\theta \)

\( \displaystyle <v_z> = \displaystyle \frac{\frac{(P_0 – P_L)\,R^2}{4\,\mu\, L}\int_0^R \left( r – \frac{r^3}{R^2}\right) d\,r}{\int_0^R r\,d\,r } \)

La integración conduce a:

\( \displaystyle <v_z> = \displaystyle \frac{\frac{(P_0 – P_L)R^2}{4 \mu L}\left( \frac{r^2}{2} – \frac{r^4}{4R^2}\bigg|_0^R\right)}{\left(\frac{r^2}{2}\bigg|_0^R\right)} \)

\( \displaystyle <v_z> = \displaystyle \frac{\frac{(P_0 – P_L)\,R^2}{4\,\mu\,L}\left( \frac{R^2}{2} – \frac{R^4}{4\,R^2}\right)}{\left(\frac{R^2}{2}\right)} \)

\( \displaystyle <v_z> = \displaystyle \frac{\frac{(P_0 – P_L)\,R^2}{4\,\mu\,L}\cdot \frac{R^2}{4}}{\frac{R^2}{2}} \)

\( \displaystyle <v_z> = \displaystyle \frac{(P_0 – P_L)R^2}{8\,\mu\,L} \) (11)

Velocidad volumétrica de flujo (Caudal).

Q = < v_z > A (12)

Área perpendicular al flujo:

A = π R² (13)

Al sustituir las ecuaciones (11) y (13) en la ecuación (12):

\( \displaystyle Q = \left[\frac{(P_0 – P_L)\,R^2}{8\,\mu\,L}\right](\pi R^2) \)

\( \displaystyle Q = \frac{\pi(P_0 – P_L)\,R^4}{8\,\mu\,L} \) (14) Ley de Hagen – Poiseuille.

Componente de la fuerza F del fluido sobre la superficie.

F_z (r) = τ_rz A (15)

De la ecuación (4):

\( \displaystyle \tau_{rz} = \left( \frac{P_0 – P_L}{2L} \right) r \) (4)

Área de contacto.

A (r) = 2 π r L (16)

Al sustituir las ecuaciones (4) y (16) en la ecuación (15):

\( \displaystyle F_{z}(r) = \left[\left( \frac{P_0 – P_L}{2\,L} \right) r\right](2\,\pi\,r\,L) \)

F_z (r) = π (P₀ – P_L) r² (17)

Para la capa de fluido sobre la superficie de la tubería r = R. Al evaluar la ecuación (17) en r = R:

F_z (R) = π (P₀ – P_L) R² (18)

Esta fuerza es equivalente a la diferencia de presión P₀ – P_L por el área de flujo π R².

Se sabe que \( \displaystyle \rho\,g + \frac{p_{0} – p_{L}}{L} = \frac{P_0-P_L}{L} \), luego:

P₀ – P_L = p₀ – p_L + ρ g L (19)

Al sustituir la ecuación (19) en la ecuación (18):

F_z (R) = π (p₀ – p_L + ρ g L) R²

F_z (R) = π (p₀ – p_L) R² + π R² ρ g L